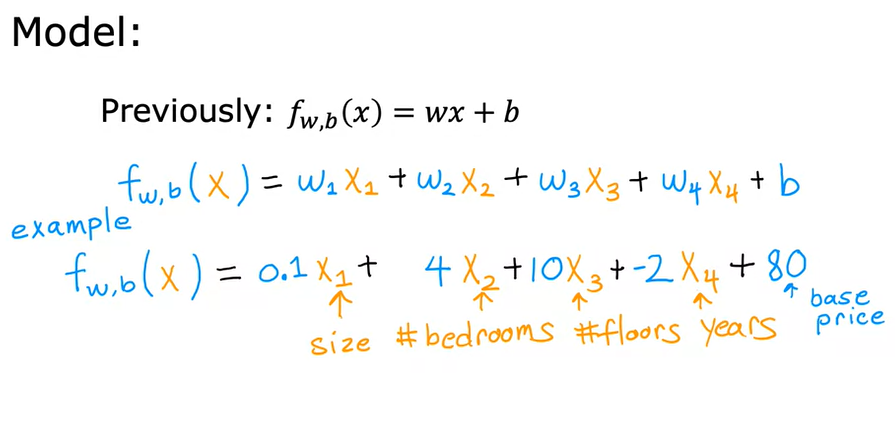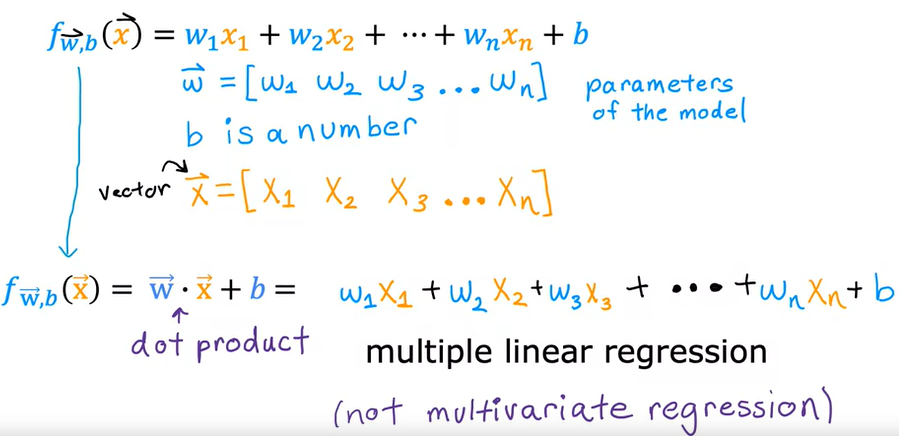Regressione lineare multipla
PREMESSA:
f(w,b) = modello
J(wb) = costo della funzione -> f (w,b) - y -> dove y sono le label
DISCESA DEL GRADIENTE = d/dw J(w,b) in sistema con d/db J(wb)
Nella regressione lineare univariata (RLS) abbiamo solo una "feature" e una corrispettiva “label”, per es. metri di un appartemento e corrispettivo prezzo.
Nel caso della regressione lineare multipla (RLM) invece, abbiamo più features a fronte di una label, per es. oltre ai metri quadrati dell'appartemento
abbiamo anche il numero di stanze, l'età dell'immobile, piano, etc etc e ovviamente come label il prezzo.
NB: la RLM non è la regressione lineare multivariata, che non conosco.
Il modello che era stato definito per la regressione lineare singola si basa sulla funzione f(x) = wx + b che in pratica definisce la funzione
(attraverso l'opportuno settaggio dei paramerti w e b tramite la discesa del gradiente) che meglio si accosta alle features/label definite per il training.
Nel caso invece della RLM, la formula diventa un polinomio del tipo (consideranto 4 features) f(x) = w1x1 + w2x2 + w3x3 + w4x4 + b
Dove x1,2,3,4 sono le features, mentre w1,2,3,4 sono i coeffienti angolari tutti potenzialmente diversi.
es:
che si può rappresentare anche:
Per risolvare questa equazione viene utilizzato il metodo della Vettorizzazione. (Vectorization)
La Vettorizzazione consente nella pratica di efettuare la moltiplicazione tra vettori/matrici utilizzando la libria numpy che sfrutta appino l'hardware della macchina.
Discesa del gradiente
Il GD a più variabili è simile a quello univariato con la differenza che al posto di un solo “w” e una sola “b” c'è un vettore di w
Il calcolo è simile se non per il fatto che bisogna iterare per il numero di features
Nella pratica la regressione lineare multipla si calcola in 2 marco step:
0) date le features e le labels di esempio:
X_train = np.array([[2104, 5, 1, 45],
[1416, 3, 2, 40],
[852, 2, 1, 35]])
matrice di 3 righe di traing con 4 colonne di features per ogni riga
e
y_train = np.array([460, 232, 178])
una riga di labels
e
dati dei valorei a caso di “w” e “b”
b_init = 785.1811367994083
w_init = np.array([ 0.39133535, 18.75376741, -53.36032453, -26.42131618])
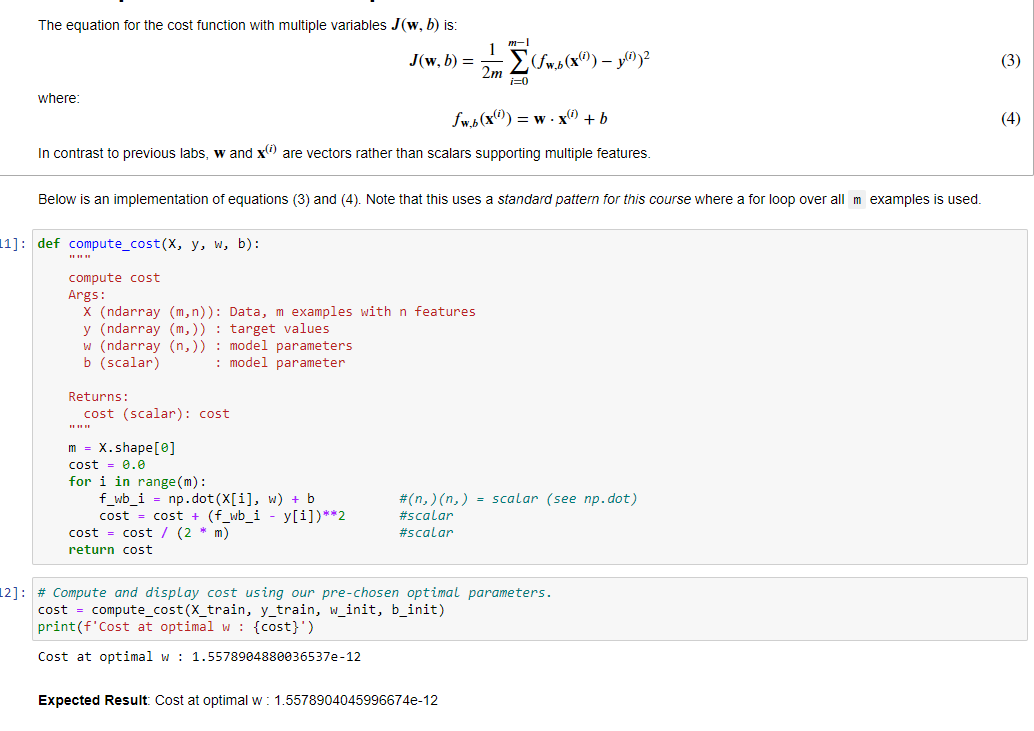
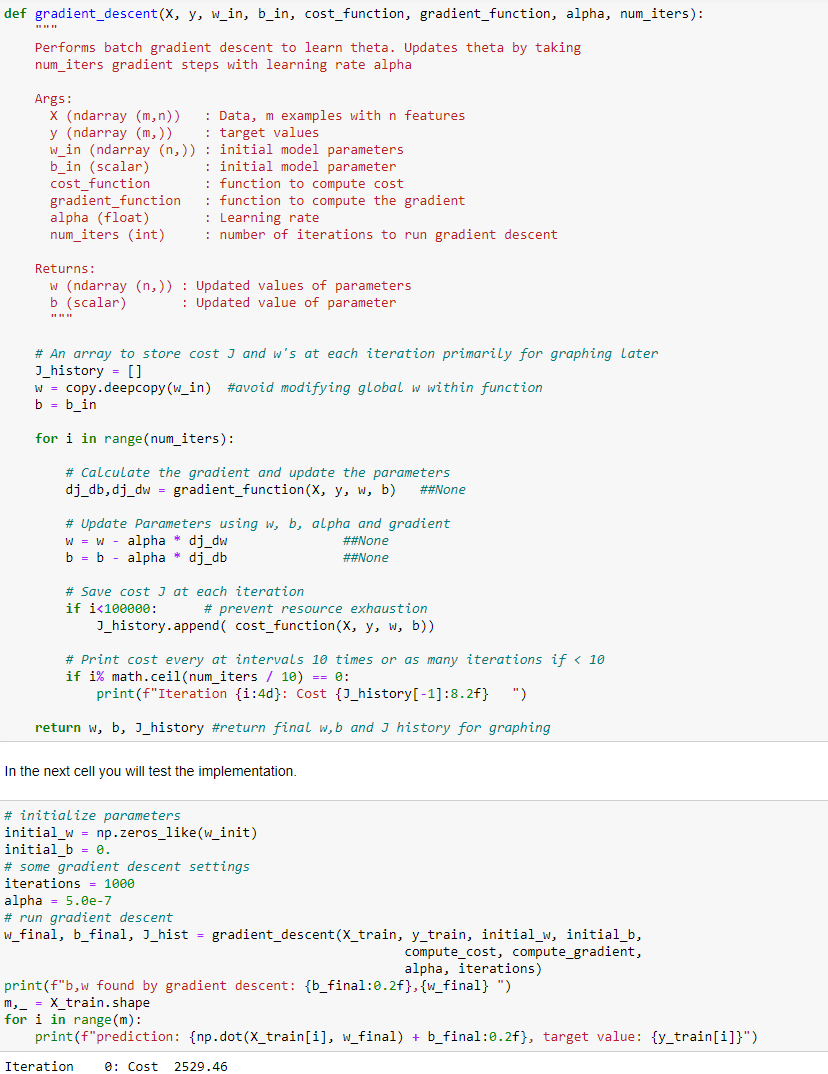
1) calcolo della funzione di costo su variabili multiple, come sotto riportato
Il metodo “compute_cost” serve per calcolare il costo della funzione per i valore w e b passati per una SOLA iterazione.
Sarà poi la fase successiva a variare i w e b richiamando poi la funzione di costo per determinare il costo totale per poi ritare “w” e “b” di conseguenza
2) Calcolo della discesa del gradiente con variabili multiple
applicando la derivata del “calcolo della funzione di costo” loopando fino a che i valore “w” e “b” minimizzano il costo
NB: ricordo che si applica il metodo della "derivata della funzione composta" accennato nella sezione “GRADENT DESCENT” relativa al paragrafo
della regressione lineare univariate.
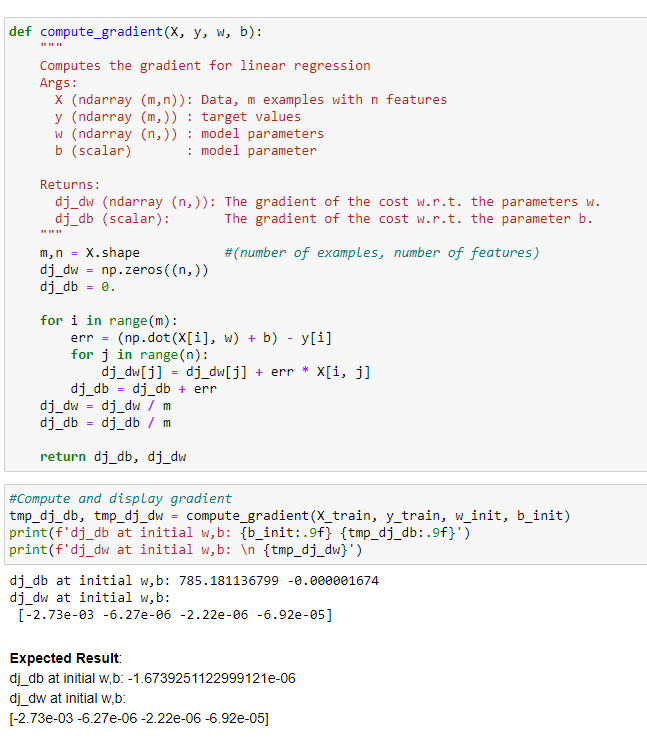
Nella pratica il calcolo delle derivate parziali in “w” e “b” si traduce in:
che viene richiamata in un loop di N iterazioni, ovvero:
In conclusione questo è la discesa del gradiente, purtroppo i risultati ottenuti non sono particolarmente brillanti, dopo
verrà illustrato come migliorare l'algoritmo.
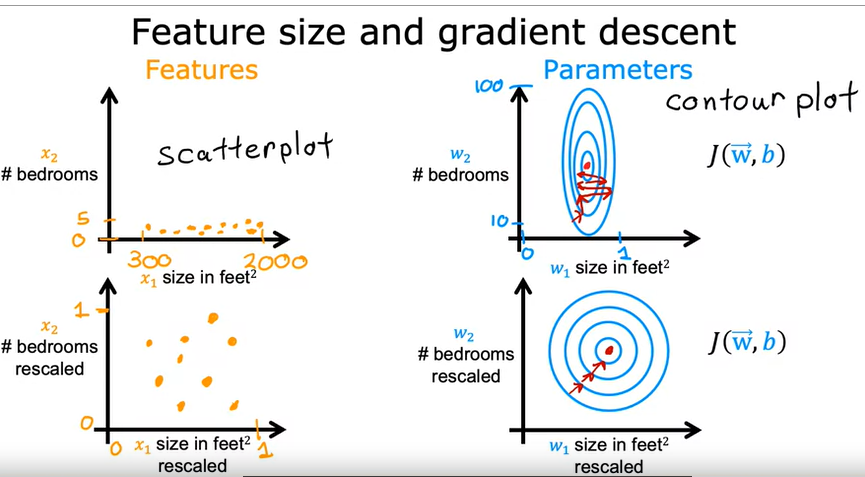
Scaling delle features e dei parametri
Nel caso in cui ci siano più features (come nella regressione lineare multipla) è importante scalare i valori delle diverse tipologie di parametri in input.
Es. se abbiamo due features come i metri quadrati e il numero di stanze di un appartmento, è bene riportare entrambi gli insiemi di valori
in un range compreso tra -1 e 1.
Il motivo è dettato dal fatto che in questo modo la regressione lineare trova più facilmente (velocemente) il suo minimo.
(vedi i grafici sotto riportati che indicano il minimo dei costi nella parte SX)
SCALING:
Le features e le label vanno quindi “normalizzati” scalandoli principalmente in questi modi:
1) dividere tutti i valori per il massimo
2) “centrando” i valori intorno allo zero applicando la formula (valori-valore medio)/(valore max - valore min)
di seguito un esempio:
un metodo ottimale per normalizzare i dati è detto Z-SCORE che riporto di seguito:
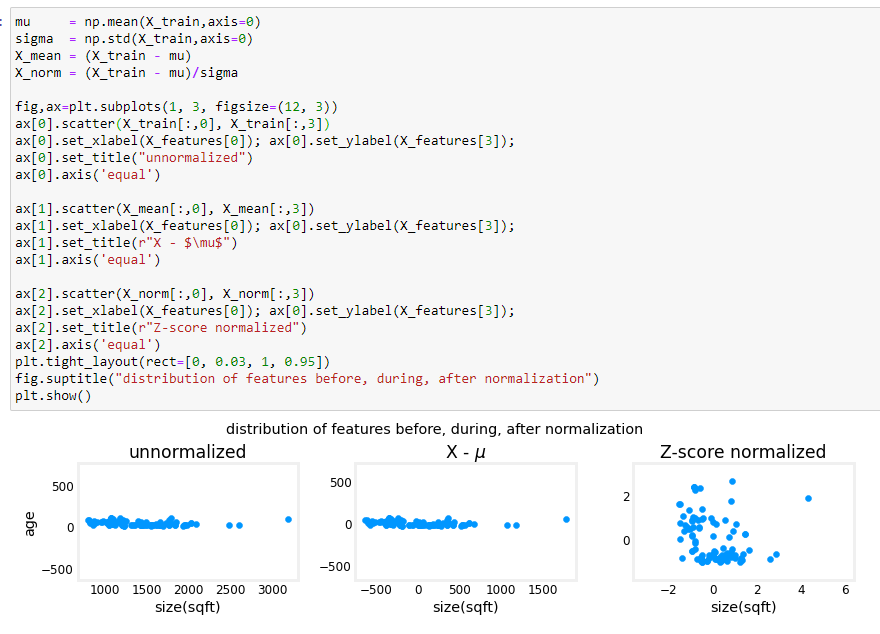
Z-SCORE
Questo metodo nella pratica va a “centrare” le features e le labels inforno allo zero. In questo modo il calcolo della regressione
lineare risulterà più veloce e più accurato nella ricerca del valore minimo relativo al costo della funzione.
DEVIAZIONE STANDARD (o scarto quadratico medio)
La DS rappresenza rappresenta la distanza dei valori di una serie rispetto alla media e si calcaola come:
1) calcolare la media dei valori -> media semplice
2) calcare la varianza dei valori -> è la differenza tra il singolo valore e la media al quadrato il tutto diveso per il totale dei campioni
3) calcolare la daviazione -> è la radice quadrata della varianza
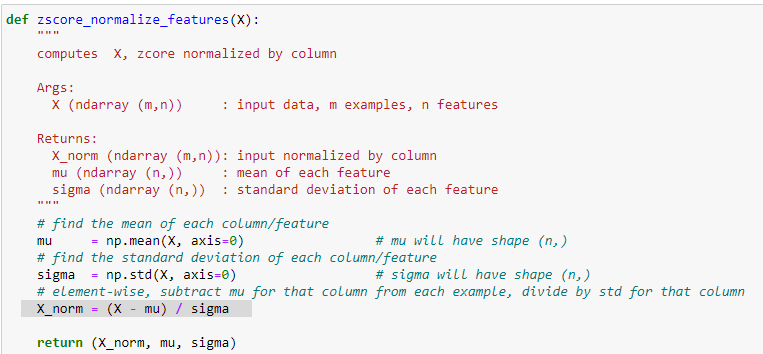
implementazione dell'algoritmo di ZScore
il cui output nell'esempio:
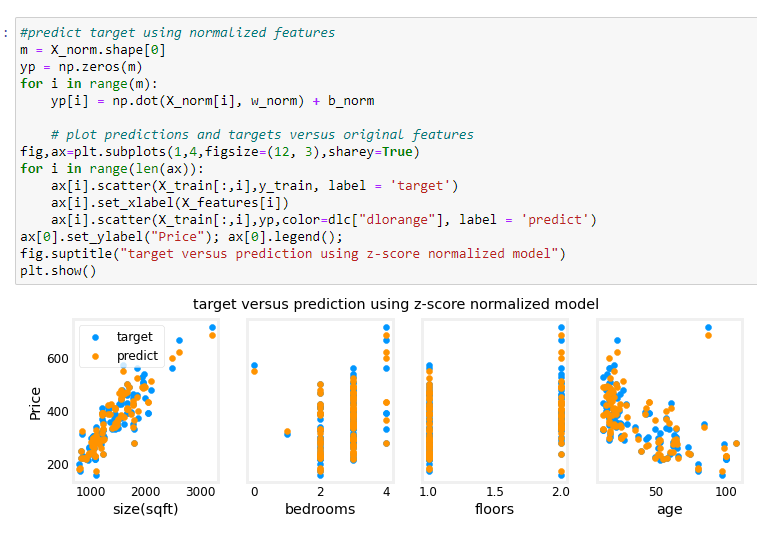
e adesso proviamo a predirre i valori.