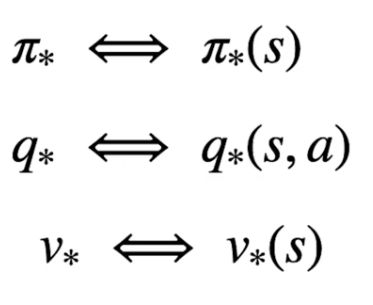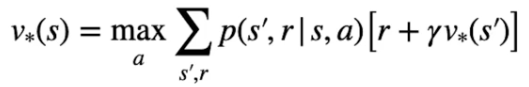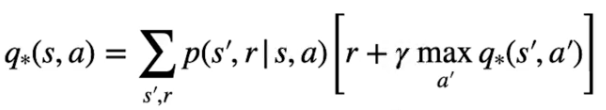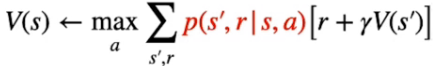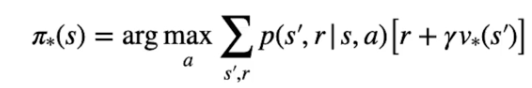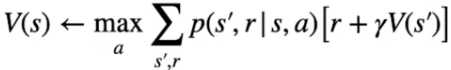Sessione 2 (Dynamic Programming)

La programmazione dinamica (aka DP) è il primo metodo in grado di risolvere il task di controllo.

Lo scopo del DP è tovare la policy ottimale π* per ogni stato V dell'ambiente (che nel nostro caso è discreto)

Per determinare quindi la policy ottimale bisogna rispettare la catena di dipendenze tra stato-azione e stato-valore, ovvero:

Nella pratica l'equazione di Bellman si dettagglia, nel caso di V* come il valore ottimable ricavato dal'azione che lo massimizza, ovvero:

e nel caso dello stato azione come la probabilità più alta che massimizzi di ritorno:

Partiamo dallo stato valore, per poter tovare il valore ottimale bisogna inzializzare tutti gli stati con dei valori a piacere, poi attraverso un processo detto di "sweep" gli stati subiscono una serie di "passate" che ne affina man mano i valori fino a farli convergere verso l'ottimo. Ogni volta che quindi aggiorniamo i valori stimati andiamo a migliorarli e per questo la nuova stima sarà megliore della precedente.

NOTA: uno dei problemi del DP è che necessita di un "modello perfetto" che descriva con precisione la transizione da uno stato all'altro, cosa che in genere non avviene nella realtà. Il modello perfetto ritorna quindi le probabilità di transizione degli stati, come evidenziato nella parte rossa della formula sotto riportata:

Un dei limiti che del DP è che parte dal presupposto che si conosca il modello e che quindi se ne possa verificare con esattezza il comportamento e quindi i ritorni. Nella realtà non è possibile fare questo, serviranno altri metodi che analizzano il comportamento dell'ambiente e cercano di stimare un modello.

Iterazione del valore (value iteration V*)

Ora vediamo l'algoritmo di "iterazione del valore" utile per determinare la policy ottimale π*. Tale algoritmo calcolo lo stato valore ottimale attraverso N passate (dette anche sweep)

Questa policy fa in modo che per ciascuno stato venga eseguita l'azione che massimizza il ritorno. Per trovare l'azione migliore dobbiamo però conoscere il valore ottimale dello stato che potrebbe seguire lo stato attuale. Per determinare il valore ottimale dobbiamo implementare un processo iterativo sugli stati, per far questo manterremo una tabella con i valori stimati per ciascuno stato. L'inizializzazione iniziale non deve essere suibito ottimale, può anche contenere valori randomici che attraverso le varie passate (sweeps) migliorano convergendo all'ottimale.

La reqola di aggiornamento degli stati sarà quindi:

Formula che tradotta significa: determinare l'azione con la probabilità più alta di ottenere la reward che massimizza il ritorno  per andare dallo stato s allo stato s'.

Di seguito lo pseudo codice che determina la policy ottimale attraverso la massimizzazioni degli stati valore:

Come si può vedere si tratta due due cicli innestati, il primo che looppa fino a che il valore precedente di ciascun stato si avvicina al valore attuale, il che significa che lo stato valore non sta migliorando più di tanto e quindi possiamo assumere una convergenza.

Il secondo loop, fa passare tutti gli stati dell'ambiente e per ciascun stato calcola l'equazione di bellman assumento  una policy di default che assegna la stessa probabilità per ciascuna azione. In questo modo a tendere alcune di queste probabilità, pur essendo uguali, andranno a trovare il ritono migliore. Nella pratica quindi per ogni stato vengono eseguite tutte le azioni possibili e considerata quella che possiede il ritorno più grande.

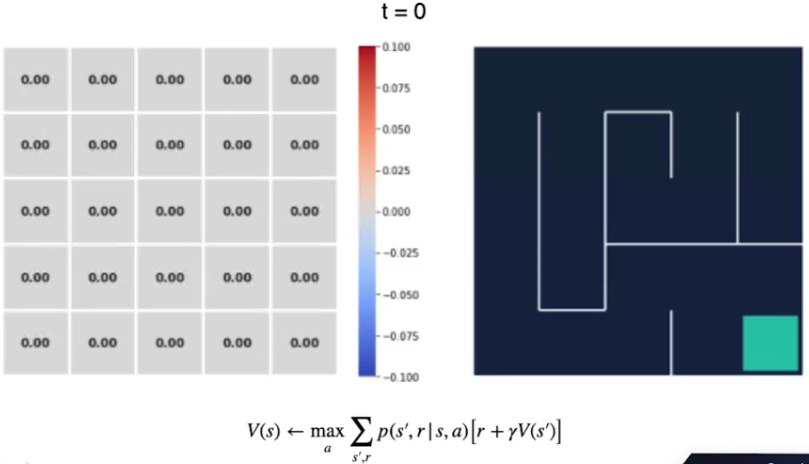
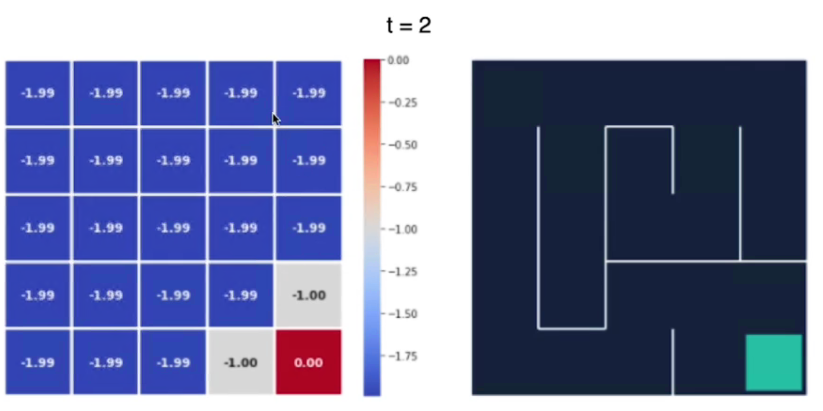
Vediamo con un esempio, qui abbiamo il labirinto di 5x5 al tempo t0 i cui valori degli stati sono inizializzati a zero. (sebbene avremmo potuto scegliere altri valori anche random)

La ricompensa per ogni azione è -1 tranne che per lo stato finale che è pari a zero.

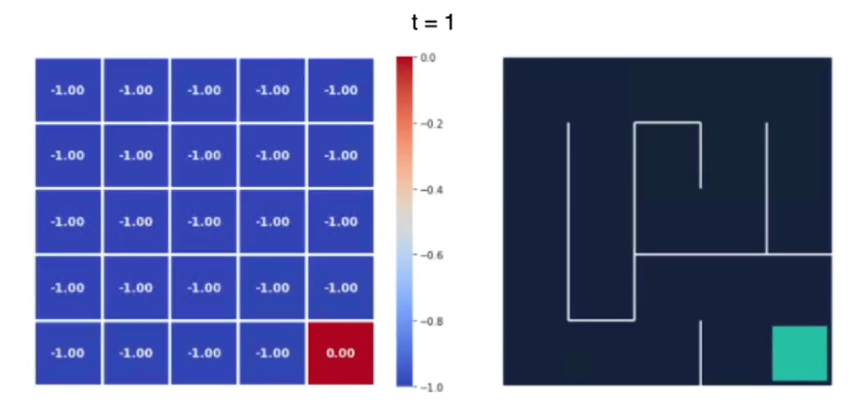
Quindi iniziamo a iterare su tutti gli stati fino all'ultimo che è quello finale, al tempo t1 il valore degli stati sarà:

si può notare come le ricompense sono tutte -1 tranne lo stato goal finale.

Al tempo t2 notiamo che il valore degli stati si "propaga" dallo stato goal a quello successivo:

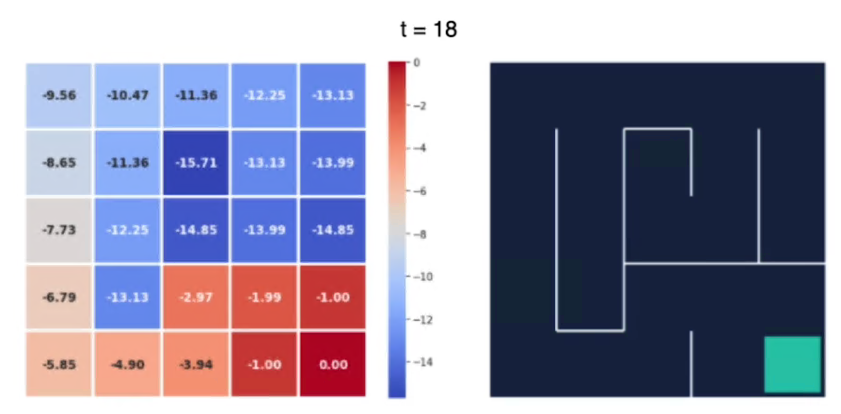
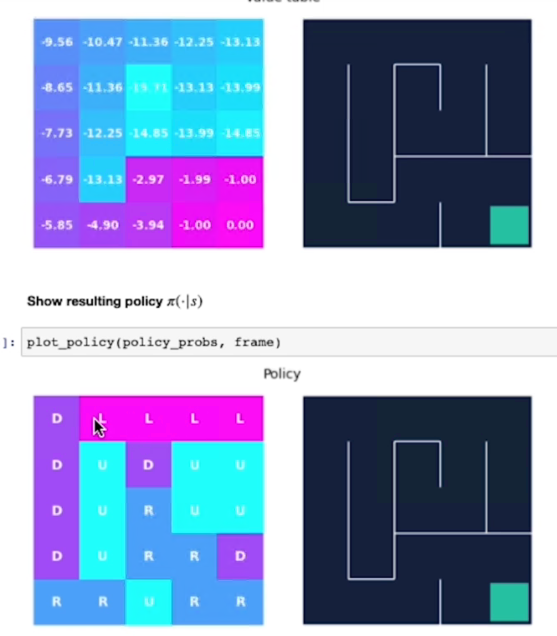
e alla fine dopo 18 iterazioni abbiamo i valori non cambiano in maniera sostanziali, siamo quindi arrivati vicini al valore ottimale:

Possiamo notare che più siamo lontani dal goal e più è basso il valore dello stato.

L'agente raccoglie più ricompense negative quando è più lontano dal goal, invece più il percorso che lo porta al goal è breve, meno saranno le ricompense negative che verrano assegnate allo stao.

Per esempio il valore -15,71 è il più alto perchè da quello stato il percorso per arrivare al goal è il più lungo.

Di seguito l'algoritmo implementato in Python:

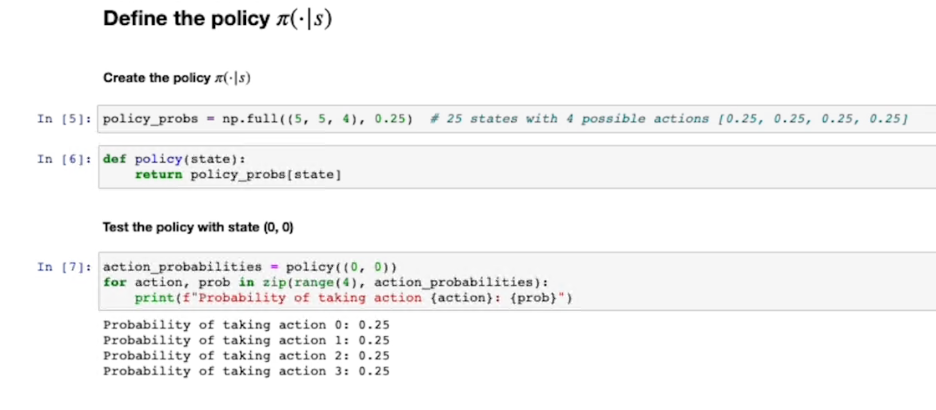
Innanzitutto definiamo la policy che inizialialmente sceglie con la stessa probabilità una azione tra le 4 effettuabili per ciascun stato del labirito:

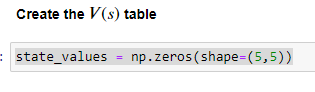
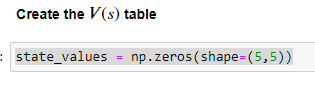
inzializziamo anche il valore degli stati:

implementiamo ora l'algoritmo che va a migliorare il valore degli stati e cambia in base al valore migliorato, la policy scegliendo quella che massimizza il risultato.

I primo while serve per verificare se il valore degli stati è arrivato alla convergenza e quindi non migliora ulteriromente.

I due for servono per sweeppare tutte le righe-colonne, mentre il terzo for innestato esegue tutte le azioni nello stato selezionato dai due for eserni.

Il cuore dell'algoritmo è nel terzo "for" interno dove per ogni azione:

• viene interrogato l'ambiete con l'azione e restituito il risultato (-1 o 0) e lo stato successivo
• viene calcolato il valore dato dall'equazione di Bellman scontata dal fattore gamma
• delle 4 azioni viene salvato il valore calcolato da Bellman più alto e l'azione ad esso associata

Fuori dal terzo "for" delle azioni possibili, viene aggiornato il valore dello stato e aggiornato l'array con l'azione associata al valore dello stato più alto calcolato con Bellman.

Viene calcolato il delta che se per tutti gli stati e tutte le azioni è inferiore ad una soglia "teta", ovvero che per tutti gli stati-valore non ci sono grandi scostamenti, allora il ciclo termina con valori e azioni ottimali.

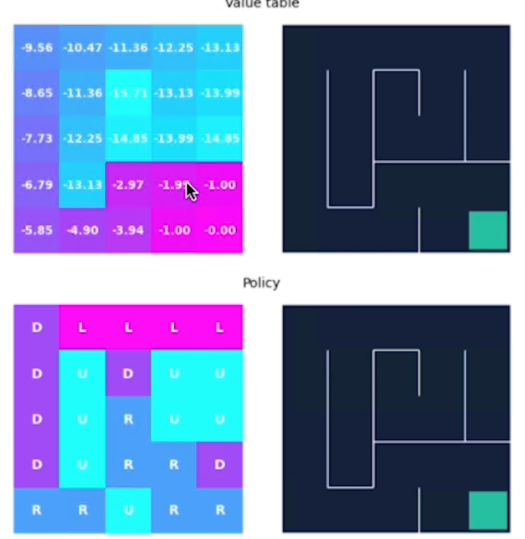
Alla fine questo è il risultato dell'algoritmo:

La policy ci porta quindi direttamente al goal.

Iterazione della Policy (Policy iteration)

Questo algoritmo evolve il precedente (value iteration) e, dal punto di vista funzionale, funge da base per futuri algoritmi utilizzati nell'ambito del Reinforcemente Learning.

I valori degli stati e della policy vengono inizializzati con dei valori arbitrari. La policy può essere per esempio definita come la probabilità equamente distribuita di effettuare una azione tra quelle disponibili.

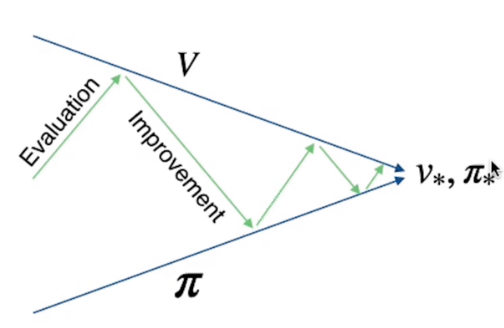
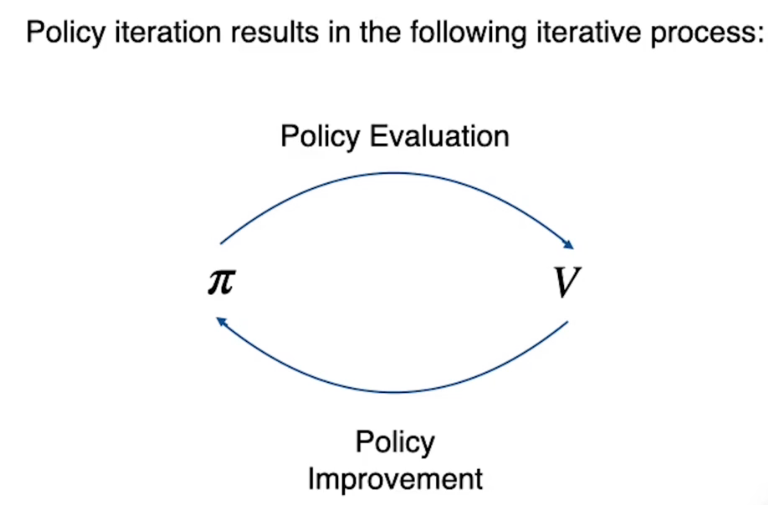
Con la policy inizializzata vengono calcolati i valori degli stati, poi, nella seconda parte, la policy viene migliorata utilizzando i valori degli stati calcolati dalla prima parte dell'algoritmo. Dopo di questo viene ripetuto il miglioramento dei valori degli stati fino a che non si giunge ai valori e alla policy ottimale.

Queste due ottimizzazioni sono in concorrenza ma nella pratica uno va ad ottimizzare l'altro alternandosi sino a giungere all'ottimale.

Di seguito il pseudo codice dove si possono notare le due fasi di ottimizzazione:

Nella prima parte che calcola il valore degli stati, il loop viene eseguito fino a che non si giunge a dei valori che risultano essere ottimali per l'attuale policy. (loop fintanto che Delta > Theta)

Da notare che, a differenza dell'algoritmo di value iteration,  dove la regola di aggiornamento dello stato era di aggiornare il valore scegliendo l'azione che massimizzava il ritorno, nella policy iteration  invece, il valore dello stato viene aggiornato sulla base delle probabilità che la policy assegna ad ogni azione. Dopo ogni "sweep" degli stati, le stime saranno sempre più vicine all'ottimale. V0 -> V1 -> V2 -> ... -> Vπ

Calcolati i volori degli stati, segue l'ottimizzazione delle policy che consiste, per ogni stato dell'ambiente,  nell'eseguire tutte le azioni possibili nel singolo stato. Per ogni azione viene applicata l'equazione di Bellman che preleva i valori dagli stati. (ricordo che il valore degli stati era stato calcolato precedentemente applicando la policy π0 che adesso stiamo aggiornando a π1)

A questo punto viene selezionata e salvata nella tabella delle probabilità associate alla policy (sempre per ciascun stato) l'azione che massimizza il ritorno secodo l'equazione di Bellman. Se dopo lo sweep di tutti gli stati, le azioni non sono variate rispetto allo sweep precedente, allora abbiamo trovato la policy ottimale e l'algoritmo si interrompe, altrimenti si rapassa all'ottimizzazione dei valori degli stati con la nuova policy appena calcolata. 

Da notare che la policy evaluation continua a looppare fino a che non trova il valore ottimale degli stati con la policy attiva, mentre la policy improvement effettua una sola passata.

 

Ora vediamo l'implementazione in Python:

anche qui, come nell'value iteration andiamo ad inizalizziare la policy e il valore degli stati:

il valore di default per gli stati sarà zero.

La probabilità di ogni azione per ciascuno stato sarà di defautl uniforme, ovvero del 25%.

Nella funzione di "Policy evaluation", viene fatta una sweep di tutti gli stati dell'ambiente, dove per ciascun stato vengono eseguite tutte le azioni che la policy mette a disposizione sommando nella varibile "new_value" i valori ottenti applicando la formula di Bellman. Si otterrà quindi una sommatoria di valori per ciascin stato, dove gli elementi della sommatoria sono le azioni dello stato applicate con Bellman. 

Il ciclo si ripete fino a che, lo sweep N ha dei valori (per tutti gli stati) che differiscono di poco rispetto allo sweep N-1 (delta > theta)

In questo caso si passa all'ottimizzazione della policy appena utilizzata, ovvero:

L'ottimizzazione della polcy prevede il classico sweep di tutti gli stati dove per ogni stato viene salvata l'azione della policy che si sta cercando di ottimizzare (che potremmo definire vecchia)

Sempre per ogni stato vengono eseguite tutte le azioni previste dalla policy precedente e tra queste scelta quella che, tramite l'equazione di Bellman, ritorna un valore più alto.

Se dopo aver effettuato uno sweep  tutte le azioni definite in tutti gli stati sono identiche allo sweep precedente, allora l'algoritmo ha trovato la policy ottimale e quindi si interrompe, diversamente si passa alla prima parte ovvero la policy evaluation.

 

Questa è la parte che messe insieme la valutazione della policy e la successiva ottimizzazione.

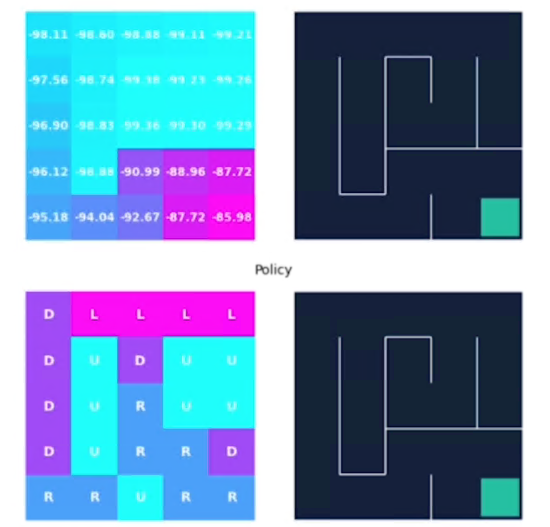
Di seguito vengono visualizzati i valori degli stati dopo il primo giro, si può notare come tali valori siano particolarmente alti in quanto la policy iniziale impostata, sbaglia molto non essedo ottimizzata. Il valore alto infatti indica il numero di passi che ci sono voluti per la policy a trovare lo stato di uscita. 

Bisogna altresì dire che, nonostante i valori alti degli stati, le azioni sono già quelle ottimali, in quanto seppur non ottilame il goal vien raggiunto.

Quelli di seuito sono già valori che si ottengon alla seconda passata con una policy che ha subito un primo processo di ottimizzazione.

Generalize Policy Evaluation

L'algoritmo di policy iterarion ci insegna che questa logica può essere mutuata come un template in molti degli algoritmi di RL attraverso la valutazione e il miglioramento della policy stessa.

Nei prossimi capitoli verranno studiati degli algoritmi più aderenti alla reatà in quanto i modelli non saranno noti (perfetti) a priori come invece avviene nella programmazione dinamica che risulta utile più ai fini didattici che pratici, senza considerate che la DP ha un alto costo computazionale. I problemi reali hanno un vasto se non infinito numero di stati, per cui questa tecnica non è praticabile.