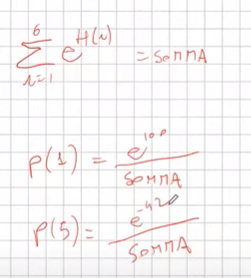Introduzione alla probabilità
Prima di procedere con lo studio del RL facciamo una breve introsuzione al calcolo probabilitico. (in particolare la probabilità elementare su insiemi finiti)
Lezione https://www.youtube.com/watch?v=o9Rc1pCYaHo&list=PLMee1hSjLKdAL16E-7EzqHXsGOgzo8iro&index=23
Cosa significa aleatorio? (sinonimo di casuale o stocastico)
E' un osservazione di un fenomeno il cui risultato non è determinabile a priori. (es. le previsioni del tempo, o il valore di un titolo azionario, o il lancio di un dado)
Pur non essendo l'esito sicuro dell'informazione si può comunque estrapolare, per es. nel lancio del classico dado otterremo un valore intero da 1 a 6 non 3,8 in virtù della tipologia del fenomeno.
La descrizione matematica che permette di affrontare questa tipologia di problemi si chiama probabilità.
Spazio campionario
Nell'ambito di un esperimento questo "spazio campionario", rappresntato dal simbolo Ω (omega), contiene tutti gli esiti possibili dell'evento che stiamo esaminando. Es. evento lancio di un dado, lo spazio compionario conterrà tutti gli esiti possibili del lancio del dato, quindi l'insime dei numeri possibili da 1 a 6. -> Ω = {1,2,3,4,5,6)
Non sempre però lo spazio campionario è un numero finito, es. il numero di accessi ad un sito web, in questo caso è l'insieme di tutti i numeri naturali, es. Ω = N0 (dove N0 è l'insieme dei numeri naturali)
Se il numero non è discreto nel caso in cui la misurazione è contina allora l'intervallo è omega comprende tutti i valori da zero a infinito, ovvero: Ω = [0, +∞)
Quindi esistono tre tiologie di spazi campionari:
- discreto finito
- discreto inifinito
- continuo
Modello probabilistico
Rappresenta la probabilità (o fiducia) che si verifichino i valori dello spazio campionario.
Es. quale è la probabilità che il numero ottenuto con il dado sia pari. (2,4,6) o la probabilità che il numero di accessi al sito web sia minore di 100.
Il RL si occupa dello spazio campionario finito. (caso 1)
Definizione: la probabilità su tutto lo spazio campionario è sempre 1. (es, quale è la probabilità che lanciando un dado esca 1 o 2 o 3 o 4 o 5 o 6 ? è il 100% ovvero 1) P(Ω) = 1. Invece la probabilità dell'insieme vuoto è zero.
Definizione: I sottoinsimi dello spazio campionario sono detti eventi. es. nel dato il sottoinsieme (evento) 1 potrebbe essere P {1,2} un altro sottoinsieme potrebbe essere P{3,4,5) e così via. Vien da se che Ω contiene tutti gli eventi possibili, NB: tutto questo vale quando gli eventi (sottoinsiemi) sono disgiunti, ovvero non si intersecano).
Suggerimento, pensiamo alla probabilità di un insieme come all'area di un cerchio, nel caso di insiemi disgiunti la probabilità dei due sottoinsiemi è semplicemente la somma, se invece i due sottoinsiemi si intersecano allora è la somma delle due probabilità meno la probabilità della loro intersezione.
Densità uniforme
Data una probabilità P su uno spazio finito e numerabile Ω, possiamo associare a P una funzione p detta densità, definita su omega valori [0,1]. Quindi la densità è definita SOLO sugli elementi di omega.
La probabilità dell'insieme che contiene il singolo elemento è funzione del singolo elemento. es. nel lancio del dadi la probabilità dell'insieme P({1,2,3}) è la somma delle probabilità dei singoli elementi che indicheremo con p minuscola ovvero: P({1,2,3})= p{(1)} +p{(2) }+ p{(3)}
ATTENZIONE: con P maiuscola ci indica la probabilità mentre con la p minuscola si indica la funzione che resituisce la probabilità. Per es. la densità definita sullo spazio campionario del lancio del dado, P: {Ω} -> [0,1] mentre la densità di ogni elemento di Ω è p(1) = 1/6... fino a p(6)= 1/6
Altro esempio
Esperimento Bernulliano
un esperimento bernulliano è una variabile che può indicare successo o non successo, è una varibile booleana. La variabile che indica la proabilità di successo è P mentre quella che indica l'insuccesso è (1-P), insieme omega è quindi Ω = {successo, insuccesso} o Ω = {1,0}
Esempio: qual'è la probabilità di ottenere un successo alla K-esima volta che facciamo un esperimento. (es. alla 10a volta)
ciò significa che per i primi 9 lanci non deve verificarsi il successo (1-P) e al decimo deve valere P. Per i primi 9 lanci le probabiltià si devono moltiplicare (1-P)*(1-P)*(1-P)*(1-P)*(1-P)*(1-P)*(1-P)*(1-P)*(1-P)*P = exp((1-P),K-1)*P
Densità non uniforme a preferenze (SoftMax)
Esistono casi in cui gli elementi dello spazio capionario hanno delle preferenze (o dei pesi) che ne alternano in qualche modo le probabilità.
NB: L'intento è quello di trasformare queste preferenze (o pesi) in probabilità. Però ci sono dei pesi negativi.
Nel caso in cui questi "pesi" abbiano valori negativi, come si calcola il peso in termini probabiliststici di ciascuno elemento di omega rispetto agli altri?
Il caso viene illustrato nell'immagine sotto riportata dove vediamo ciascuno preferenza H definita per ciascuna delle 6 facce delle dado. Si può notare che esistono delle preferenze negative che se dovessimo calcolare semplicemente come peso della singola preferenza fratto sommatoria di tutti i pesi, ne risulterebbe una probabilità negativa.
Quindi per es. se volessimo calcolare la probabilità di P(H1) sarebbe -> 100 / (somma di tutti i pesi) . Però non funzionerebbe in quanto abbiamo dei pesi negativi, e nel caso per es. di P(H3) verrebbe una probabilità negativa, il che sarebbe sbagliato.
Per nornalizzare questi valori si applica semplicemente la funzione esponenete per ciascuna preferenza che rende tutti i numeri > 0. (anche con esponente negativo i valori sono sempre > 0) quindi diventa. (non considerare la variabile beta)
Q quindi diventa:
Questa tecnica per normalizzare i pesi è detta softmax. E' importante perchè la somma delle probabilità di tutti i valori "pesati" da 1.
Nel caso di insiemi discreti non finiti si applicata la formula Poisson. (che in questo momento non ci interessa)
Contare le combinazioni di eventi complessi
Supponiamo di poter filtrare un insieme per determinare caratteristiche che si sommano in successione.
Utilizziamo degli esempi:
1) voglio determinare le carte pari di cuori e picche da un mazzo di carte di poker:
Applico la regola delle caratteristiche che si sommano,
In questo abbiamo 2 caratteristiche, ovvero:
caratteristica 1) le carte pari ->5 su 13
caratteristica 2) i semi di carte -> 2 su 4
quindi sommiamo la caratteristica 1 e 2 che matematicamente significa moltiplicare, ovvero: 5*2 = 10
2) sempre la mazzo di poker voglio trovare tutte le combinazioni di full possibili. (3 carte dello stesso valore + 2 dello stesso, esclusi vicendevolmente es. 3 carte di assi + 2 carte di jack)
In questo abbiamo 4 caratteristiche, ovvero:
caratteristica 1) 3 carte uguali -> 13
caratteristica 2) 2 carte uguali (in quanto vado ad escludere il tris) -> 12 (in quanto non possono esistere 5 carte con lo stesso valore)
caratteristica 3) 3 carte che hanno 3 semi su 4 -> 4 presi in combinazione di 3 (combinazioni semplici senza dipetizione C(4,3)
caratteristica 4) 2 carte che hanno 2 semi su 4-> 4 presi in combinazione semplice senza ripetizione C(4,2)
= 13*C(4,3)*12*C(4,2) = 3744
Calcolo combinatorio
Di seguito un breve ripasso del calcolo combinatorio
Disposizioni semplici
Le disposizioni prese da un insieme di N elementi in K modi (es. da un insieme di 10 numeri (N) presi a 2 (K) ) sono un sottoinsieme di numeri ordinati, dove l'ordine del numero conta, allora la formula diventa N! / ( N-K)!
Combinazioni
Se invece l'ordine dei non conta allora il numero di casi dimunuisce quindi la formula diventa N! / K! * (N-K)!
Probabilità condizionata
Premessa: l'informazione cambia le probabilità.
Premessa bis: La proababilità ovviamente si calcola come casi favorevoli fratto casi possibili.
Es, qual'è la probabilità che lanciando un dado esca il numero sei? ovviamente 1/6. Supponiamo invece che dopo aver lanciato il dado qualcuno ci dica che è uscito un numero pari, ora come cambia la probabilità? in questo caso lo spazio campionario (omega) cambia e passa da sei numeri a tre tutti pari, a questo punto la proabilità diventa 1/3.
Sia un evento A condizionato a B -> P (A | B) il calcolo diventa P(A|B) = P(A ∩ B) / P (B)
Indipendenza di eventi
Premessa: In genere sapere il verificarsi di un certo evento ci da informazioni sulla probabibilità di un altro evento.
Ci sono però casi che l'informazione non modifica che la probabilità che modifichi l'evento.
Quindi P(A|B) = P(A) significa che se la probabilità di A condizionata all'evento B è invariata allora i due eventi sono indipendenti.
L'intersezione dei due eventi rende la probabilità una funzione moltiplicazione, ovvero: P(A ∩ B) = P(A) * P(B)