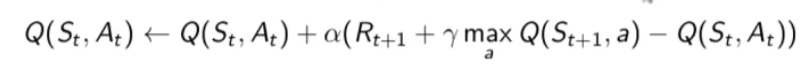Sessione 2

Metodi Model free

Nel capitolo precedente abbiamo svolto un lavoro di pianificazione e non di appredimento per rinforzo in quanto avevamo il modello (ambiente) che ci diceva con quale probabilità svolgeva le azioni. La policy (pi) era in qualche modo nota, questo però non rappresenta la realtà in quanto il modello, nella natura delle cose, non ci viene dato a priori, dobbiamo quindi trovare un modo per ricavarlo, come fare? Bene bisogna quindi interrogare l'ambiete e con le risposte ottenute ricavare in quale modo il modello. Abbiamo quindi a che fare un metodi "model free" in quanto il modello NON è noto a priori.

Da notare che possiamo comunque interagire con l'ambiente tramite esperienza,  ovvero:

1.  parto da uno stato che posso scegliere in maniera casuale
2. scelgo l'azione tramite la mia policy e vedo cosa succede
3. torno al punto 1 e così via fino alla fine dell'episodio
   

SPIEGONE: Tutto questo fino a quando otterremo la "policy ottimale", ovvero facendo la media di tutti i ritorni Gt. Quindi per via delle legge dei grandi numeri possiamo approssimare il valore medio atteso () con la semplice media empirica. Ricordo che il valore atteso (E) è quello che si calcola con le probabilità di transizione, mentre la media empirica è la semplice somma di tutti i valori diviso il numero totale dei valori. Quindi quando il numero di valori tende a infinito allora il valore converge al valore atteso.

Predizione

E' model free perchè non abbiamo a priori il modello, cosa che invece avevamo all'inizio del corso con la pianificazione.

Dovremo quindi far uso di "stimatori" in grado di ricostruire nella maniera più federe possibile il modello.

Dobbiamo quindi fare un lavoro di predizione, per fare questo abbiamo due metodi, il primo detto "Monte Carlo" mentre il secondo detto "Temporal Difference"

Metodo Monte Carlo 

Il metodo Monte Carlo (MC), nella pratica voglio "imparare" il valore delle mie azioni iteragendo con l'ambiente. Banalmente compio azioni "a caso" e poi tengo traccia delle media aritmetica degli episodi che faccio. Svolgo quindi un episodio partendo dallo stato k e raccolgo tutti i valori, e relative reward, degli stati fino allo stato terminale. Terminato un episodio G(T) ne faccio altri N, poi, per ottnere il valore V(Sxx) faccio la media aritmetica di tutti i G(T) ottenuiti partendo dal quello stato "S"  e salvo il valore ottenuto nello stato s. Svolgo questo lavoro per N volte per tutti gli M stati, in questo modo a tendere, sempre per la legge dei grandi numeri, mi avvicino al valore reale dello stato. (da notere che con questo metodo non devo inizializzare gli stati in quanto interrogo subito l'ambiente) 

NB: MC è un metodo "off line" ovvero che impare dopo aver finito l'episodio.

Questo metodo impara il valore della policy dall'esperienza. 

Da qui deriva il concetto di "boostrapping", ovvero quando calcolo il valore Vk applicando la funzione "one step looking ahead" andando ad esplorare gli stati successivi s', utilizzo i valori Vk calcolati in precedenza per ricalcolare l'attuale valore Vk.

Da notare che nei metodi con bootstrapping bisogna stimare i valori di tutti gli stati altrimenti perde efficacia.

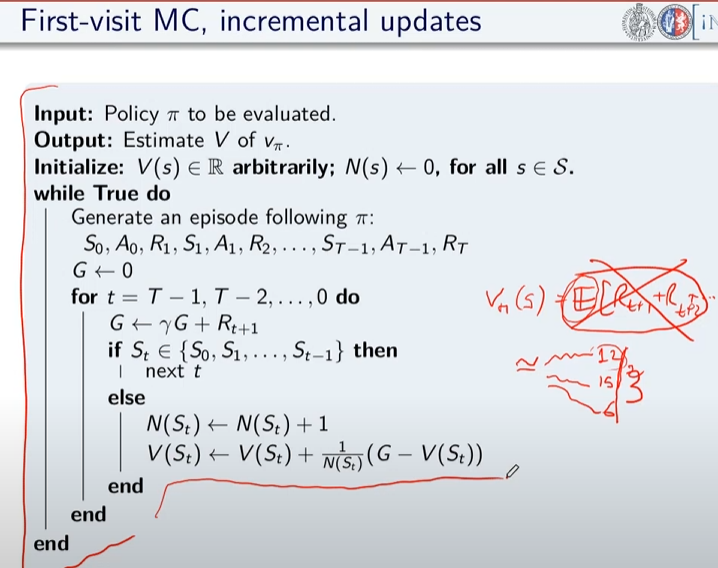
Di qui la versione più semplice dell'algoritmo in pseudo-codice:

da notare la formula sottolineata che rappresenta la forma incrementale della media aritmetica, ovvero come aggiungere un valore ad una media considerando il suo peso rispetto alla media stessa. In pratica si tratta di sommare la media a (valore meno la media)/numero totale dei valori.

come funziona: 

• inzializza la funzione valore con dei valori a caso (anche zeros)
• facciamo un episodio, ovvero memorizzare:
  • tutti gli stati
  • tutte le azioni
  • tutte le ricompense 
  • fino alla fine
• partiamo dalla fine dell'episodio (stato Rt) e inzializziamo il valore Gt a zero
• procedo risalendo gli stati partendo da quello terminale che vale zero, vado a T-1 del quale prendo la ricompensa e la sommo a quella dello stato se segue (in questo caso quello finale) 
• procedo risalendo in questo modo (sommando) fino allo stato iniziale
• calcolo il valore V(St) come la media dei ritorni di tutti gli stati precendenti (da quello terminale a quello in elaborazione)

Di seguito il codice che implementa l'algoritmo:

import io
from collections import defaultdict

import numpy as np
import sys
import gym
import matplotlib as plot

"""
Il BJ è un gioco a due o più giocatori, si tratta di uno o più giocatori contro il banco.
Il banco mostra una carta e poi ci da 2 carte, noi sommiamo queste due carte e possiamo decidere
se prendere una carta o rimanere fermo (stick)
Quando mi fermo faccio la somma delle mie carte, se ho più vi 21 punti allora ho perso, se invece meno
tocca al banco e lui continua a prendere carte fino a quando arriva ad avere più o uguale 17 punti.
A quel punto si ferma anche lui e chi ha di più vince.
NB: Il banco non è interessato a quello che facciamo noi.

POLICY: continuiamo a prendere fino a quanto arrivo a 20 o 21, la reward è +1 se ho vinto, -1 se perdo o zero se pareggio.
Il valore dello stato non è più la probabilità della vittoria

"""

env = gym.make("Blackjack-v1", sab=True)


def mc_prediction (policy, env, num_episodies, discont_factor =1.0):
    """
    Algoritmo di predizione Monte Carlo, calcola la funzione valore per una data policy utilizzando il metodo "sampling"

    :param policy: una funzione che mappa un'osservazione ad una azione probabile
    :param env:  openAI gym
    :param num_episodies:  numero di epidosi che compongo il sample
    :param discont_factor: solito

    :return: un dizionaio che mappa lo stato nel valore valore, è una tupla il cui valore è float
    """

    # preparo il dizionario di ritorno delle funzione
    # tiene traccia e conta i ritorni di ciascuno stato per calcolarne la media
    # NOTA: tale metodo è inefficiente
    returns_sum = defaultdict(float)
    returns_count = defaultdict(float)

    # funzone valore finale
    V = defaultdict(float)

    for i_episode in range (1,num_episodies+1):
        # stampo a quale episodio mi trovo (utile per il debug)
        if i_episode % 1000 == 0:
            print("\repisode {}/{}.".format(i_episode,num_episodies), end="")
            sys.stdout.flush()

        # genera un epidosodio rappresentato da un array di tuple composte da (stati, azionie e ricompendse)
        episode = []
        state, info = env.reset() # resetto il gioco ovvero la carta che viene mostrata dal banco + le 2 carte che abbiam
        while True:
            probs = policy(state) # probabilità della policy
            # scelgo un'azione a caso dalle prob. della policy
            action = np.random.choice(np.arange(len(probs)), p= probs)
            next_state, reward, done , truncated, info = env.step(action)
            episode.append((state, action, reward))
            if done:
                break
            state = next_state

        # scorro tuti gli stati visitati nell'episodio e calcola il valore medio per ogni stato
        states_in_episode = set ([tuple(x[0]) for x in episode])
        for state in states_in_episode:

            first_occurence_idx = next(i for i,x in enumerate(episode) if x[0] == state)

            G = sum ([x[2]*(discont_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
            returns_sum[state] += G
            returns_count[state] += 1.0

            # media aritmetica
            V[state] = returns_sum[state] / returns_count[state]

    return V

def sample_policy(observation):
    """
    la policy che "sticks" ovvero si ferma se il punteggio del giocare è >= 20, altrimente prende una carta
    :param observation:
    :return:
    """
    score, dealer_score, usable_ace = observation
    return [1,0] if score >= 20 else [0,1]

V_10k = mc_prediction (sample_policy, env, num_episodies=10000)

Metodo Temporal Difference

Il mtetodo Temporal difference (TD). E' un metodo iterativo, per prima cosa devi inizializzare tutti gli stati con dei valori che potrebbero anche essere random. Partendo dallo stato s faccio una sola azione per arrivare nello stato s+1 e raccolgo il valore dello stato e la rimpensa corrispondente all'azione. Torno quindi allo stato in cui ero parito allo step (s) e aggiorno il valore. Come aggiorno il valore di S? V(s) = V(s) + α(R + ɣV(s+1) - Vs) dove α è il fattore di apprendimento, più è grande più do importanza al valore restituito dallo stato s+1. Il che significa sommare il valore dello stato attuale alla somma data della reward più la differenza tra il valore dello stato successivo e il valore dello stato attuale, il tutto moltiplicato per il tasso di apprendimento alpha. Da notare che la differenza tra V(s) e α(R + ɣV(s+1) - Vs) è detta errore, che posso variare con il tasso di apprendimento alpha.  Poi si continua passando allo stato successvo e faccio la stessa cosa aggiornando V(s+1) con i valori ricavati da V(s+2). Anche quindi come con il MC faccio passare tutti gli stati S e lo faccio per N volte, anche in questo modo i valori  convergeranno, dopo un numero considerevole di volte, al valore reale.

Esempio.

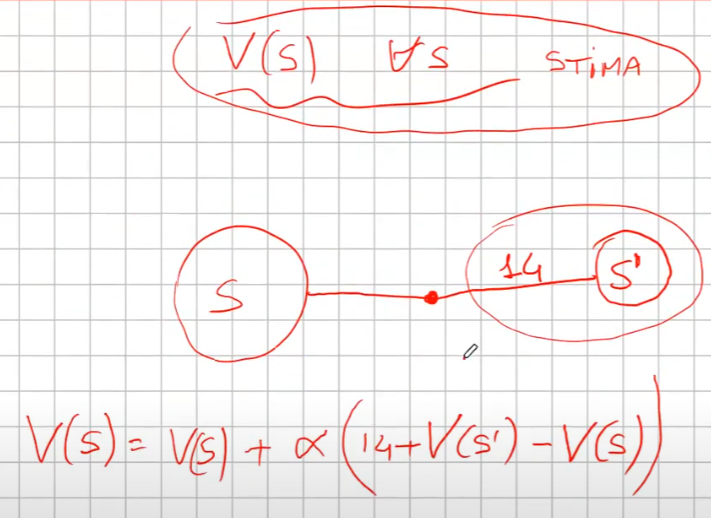
1. setto dei valori a caso per tutti gli stati  (es, zero per tutti)
2. ad ogni passo sapendo che ho una stima per ogni stato mi metto nello stato di partenza S
3. nello stato V(S) faccio l'azione arrivando nello stato S' ottenendo 14 di ricompensa
4. la mia nuova stima di V(S) sarà quindi la ricompensana + il valore di S' -> R+V(S') che essendo all'inizio V(S') varrà zero però.. 
5. la stima nuova non voglio utilizzarla completamente per inserirla nello stato S cerco quindi di "poderarla" in qualche modo, quindi sottrarò dalla stima il valore dello stato S ovvero V(S) che in gergo si chiama errore e lo sommo al valore di S.
6. Riassumendo V(S) = V(S) + α(errore)  dove l'errore è (R(S') + V(S') - V(S))
7. faccio così per tutti gli stati

dove α è un iperparametro (numero) che rappresenta quanto viene valutata affidabile la stima

Nella pratica cerco di pesare il valore di V(S') tramite l'iperparametro α in considerazione del valore V(S')

NB: qui faccio del boostrapping, ovvero ad ogni passo aggiorno le stime utilizzando le stime del passo precedente.

Di seguito lo pseudo-codice per la predizione.

Dove ad ogni passo aggiorno il valore della funzione valore. 

Differenze e analogie tra MC e TD

• MC funziona solo quando il task è episodico. (quando l'episodio finisce, in realtà esistono task infiniti) TD funziona anche con task continuativi. Nel metodo MC bisogna vedere i ritorni di tutti gli episodi, nel TD invece stiamo stimando il valore di uno stato usando la stima che avevamo prima. Ovvero, al passo K+1 si stimano i valori degli stati usando i valori del passo K e per questo motivo si parla di "differenza temporale". TD apprende ad ogni passo, MC invece deve finire l'episodio. TD è un metodo ON-LINE ovvero che impara ad ogni passo, mentre MC è un metodo OFF-LINE perchè ha bisogno di finire l'episodio aggiornare le sue stime.
• Il MC sommando tutti i ritorni rischia di avere una varianza molto alta in quanto i ritorni potrebbero variare inducendo un ampliamento totale dell'errore, per contro il TD non sommando tutti i ritorni, in quanto si ferma al solo stato successivo, riduce la varianza dell'errore quindi converge prima.
• TD è distorto, mentre MC non lo è.. un punto a favore di MC

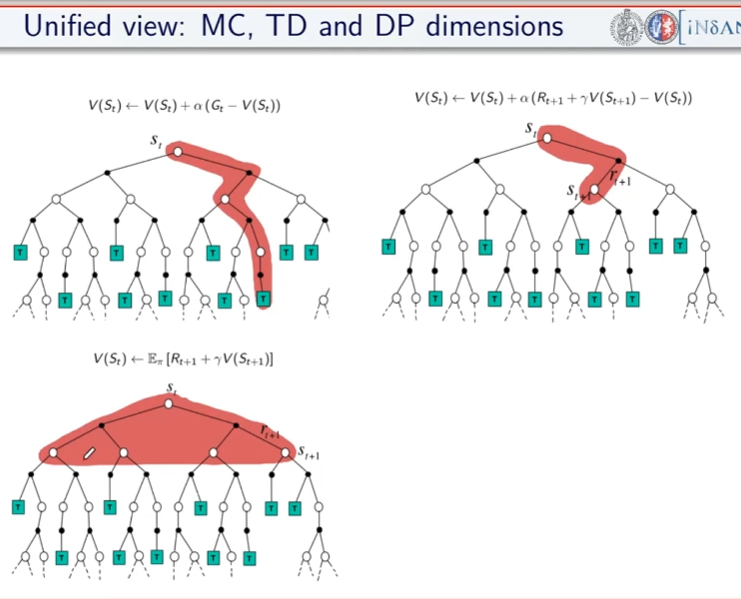
Curiosità: diffrenze tra MC , TD e programmazione dinamica (vista a inizio corso)

Model free -> miglioramento e controllo

Nella predizione, viene sempre applicata la stessa policy, ovviamente anche la policy deve migliorare nel tempo, ecco che quindi dopo il ciclo di predizione deve seguire il ciclo di miglioramento e controllo della policy. Questo significa che i valori  degli stati migliorerano nella fase di predizione e che la scelta degli stati stessi, conseguenza del miglioramento della policy, cambia in quanto le azioni cambiano (in genere) con il cambio della policy per via del miglioramento della stessa.

Esistono due famiglie di metodi per fare miglioramento e controllo, e sono:

1. On-policy MC control (controllo = iterazione del miglioramento con la predizione)
2. On-policy TD control (controllo = iterazione del miglioramento con la predizione)
3. Off-policy prediction
4. Off-policy control 

Che differenza c'è tra i metodi on-policy e off-policy?

On-policy

Questi metodi nella pratica utilizzano la stessa policy migliorandola. Ovvero agendo "greedy" vengono scelte le azioni che massimizzano il risultato e che ne migliorarno la policy, ma, la policy seppur migliorata è sempre la stessa.

Off-policy

Con i metodi off-policy viene introdotto un fattore di "esplorazione" che in qualche modo crea delle policy nuove "parallele" a quella che stiamo migliorando, per poi metterle in qualche modo a confronto ed eventualmente cambiare la policy con quella nuova trovata tramite esplorazione.

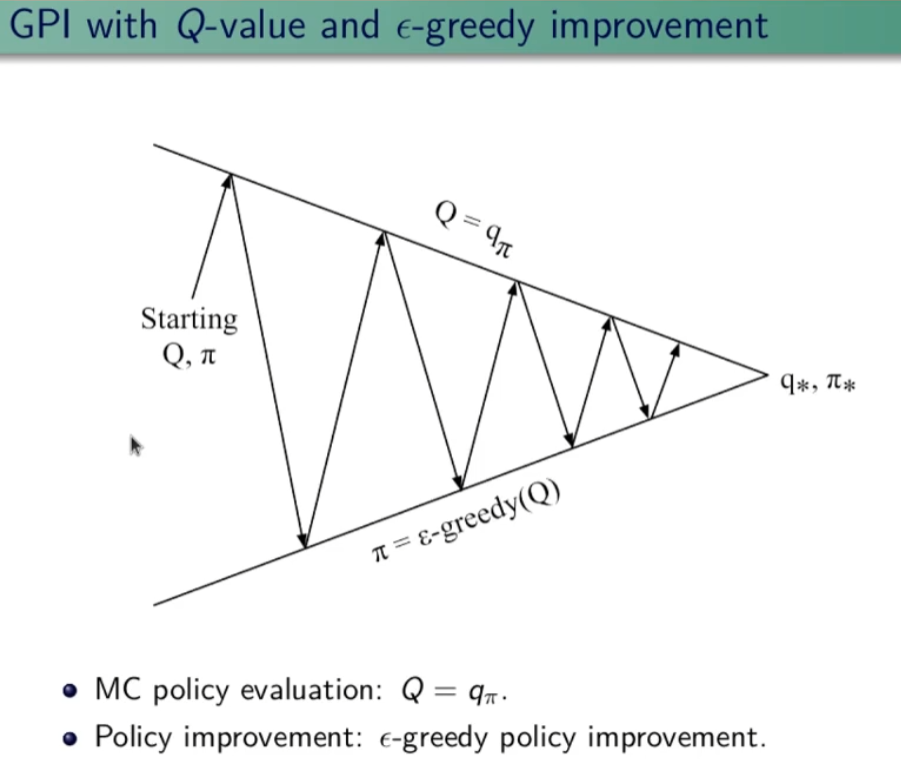
General Policy Iteration

Come miglioro la policy? Basta fare il calcolo della funzione valore stato-azione Q(s,a) anzichè il valore della stato azione V(s) in modo da ottenere la probabilità dell'azione. Ok, ma questo non serve realmente per migliorare la policy in quanto agisce sempre in manidera greedy sulla stessa policy. Per migliorare la policy quindi è necessario scegliere "ogni tanto" delle azioni che non sono greedy in modo da effettuare l'esplorazione. Ricordo che per miglioramento della policy si intende: "il valore della nuova policy è migliore della precedente in tutti gli stati".

Dilemma dell'esplorazione vs sfruttamento

Di qui il metodo "epsisodio greedy" (ε-greedy) , dove epsilon è la percentuale di scelta di una azione casuale. (in genere un valore piccolo es. 10%)

Bisogna quindi lavorare con policy stato-azione con probabilità > 0 in particolare la percentuale deve essere maggiore di ε. (questo concetto non mi è chiaro)

GL-IE (teorema generale)

Come deve funzionare l'algoritmo epsilon greedy? L'algoritmo da utilizzare è il GLIE che, per definizione, converge alla policy ottimale, ma cosa significa GLIE e come funziona?

GL= greedy in the limit: si richiede che nella policy iteration (valutazione della policy e miglioramento) che il miglioramento tenda ad una policy greedy. Che significa che la policy a cui si converge è greedy.

IE= infinite exploration: tutte le coppie stato-azione siano visitate dall'algoritmo infinite volte. (richiesto dalla legge dei numeri)

Se GL e IE sono confermati ed implementati allora l'algoritmo è ottimale.

Ma come fare? La risposta è implementare l'algoritmo espisolon-greedy facendo in modo che epsilon decresca al crescere degli episodi k. Il che significa che ad un certo punto epsilon tenderà a zero.

On-policy MC (Monte Carlo)

Per calcolare la policy  e migliorarla va usato il Q-Value.

Partenze esplorative (exploring starts)

Un altro algorino GLIE è per es. quello che implementa le "partenze esplorative" ovvero la scelta causale di uno stato di partenza.

On-policy TD (temporal difference)

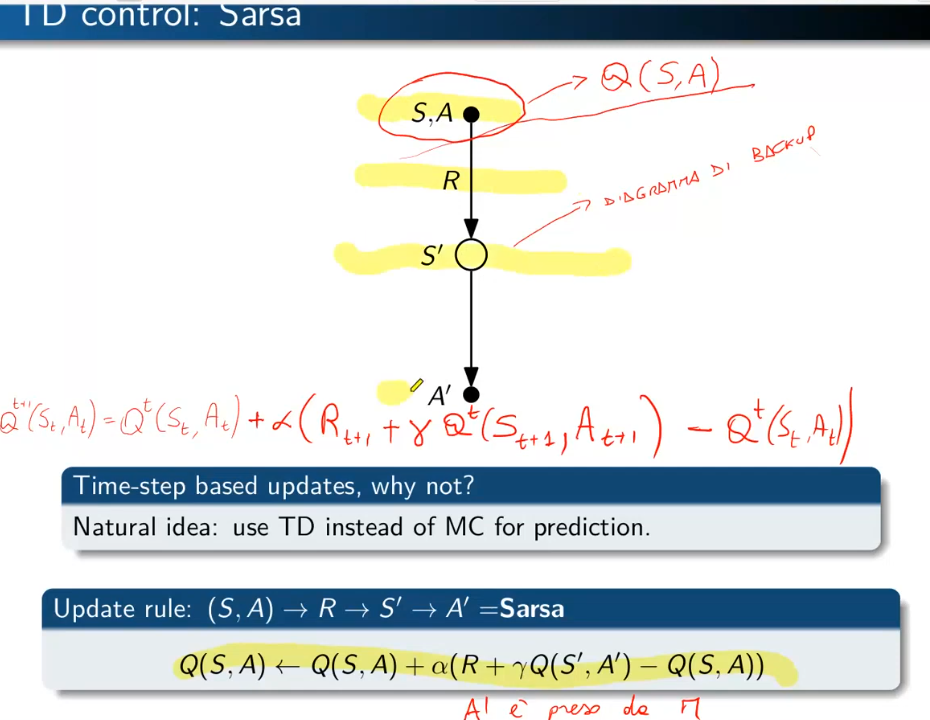
Anche per il TD dovremmo utilizzare il Q-Vaue, l'algoritmo da utilzzare si chiama "Sarsa".

Si chiama così perchè parte dalla coppia Stato-Azione vede ricompensa abbiamo ottenuto, vede lo stato successivo ottenuto, prende una nuova azione (quindi va in un nuovo nodo Stato-Azione) e si ferma. Ricordo che il concetto di stato stato nel "model free" è sempre riferito allo Stato-Azione. (vedi diagramma di backup sotto riportata)

Predizione

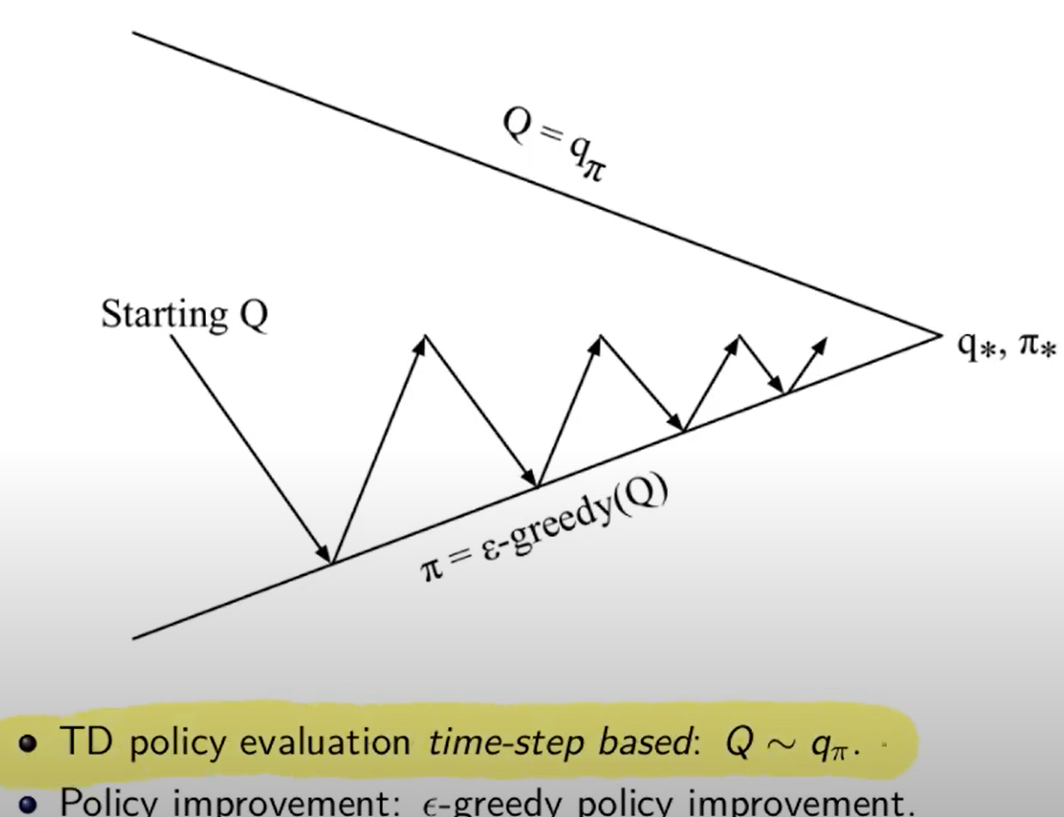
Per la fase di predizione TD, quando arrivo nel nuovo nodo vedo il valore Q-Value associato allo stato-azione di arrivo. Anche qui vale la formula classica di calcolo del valore stato per TD con la differenza che, essendo model free, dovremo utilizzare il Q-Value e quindi la combianazine Stato-Azione. Anche qui alpha rappresenta il fattore di apprendimento, la tabella dei q-value va anche qui va inizializzata con valori a piacimento, alla fine dei vari episodi il tutto dovrebbe convergere.

e quindi il diagramma di convergenza

e lo psudo-codice:

Scegliamo il tasso di apprendimento (alpha), inizializziamo la tabella degli stati-azioni facendo attenzione a impostare il valore dello stato terminale a zero. (altrimenti avremo una distorsione nel valore iniziale che non verrà mai corretta)

Controllo epsilon-greedy

Per migliorare la policy utilizzo il metodo epsiolo-greedy ovvero partendo dalla matrice dove ogni cella contine il valori stato-azione... 

Scegliamo la partenza, scegliamo un'azione dallo stato S utilizzando una policy epsilon-greedy. Quando lo stato è terminale riconciamo.

Funziona? si purchè siano soddisfatte delle ipotesi (teoriche) che sono:

1) la successione di policy che ottengo devono tutte darmi tutte esplorazini infinite (soft) e devono essere greedy-in-limit, ovvero con espilon-greedy non costante, cioè che deve tendere - all'aumentare di k - al valore zero

2) il tasso di apprendimento alpha che tende allo zero velocemente ma non troppo..

Però queste due condizioni teoriche non vengono quasi mai rispettate, quindi in genere si tengono come costanti

Esiste anche al versione a N step di Sarsa:

e questo lo pseudo codice:

Metodi off-policy

Con il metodo off-policy usiamo una policy "u" (mu) detta di "esplorazione" per fare un'esperienza (traiettoria) che ci dice come è fatto l'ambiente, uso questa esperienza per valutarne un'altra detta policy "target" "pi" (di miglioramento) e le confronto. Quindi nella pratica c'è una policy che impara e una che fa esperienza. (esperinza detta anche policy comportamento)

Difetti

• questi metodi hanno una varianza molto alta e quindi convergenza molto lenta
• quando utilizzati + metodi non tabellari (rete neurali) + bootstrapping = non funziona

Vantaggi

• risolve il dilemma esplorazione-sfruttamento molto bene
• l'esperienza pregressa può essere acquisita (importata) dall'esterno ed essere sfruttata
• posso riusare quando voglio le esperienza generata nelle policy precedenti
• posso imparare policy multiple ovvero seguo una policy da questa ne derivo N che possono essere tutte ottimali

Prerequisito di utilizzo

Se un'azione ha probabilità positiva di essere scelta allora deve essere positiva anche la probabilità di scelta di un'azione della policy di comportamento, ovvero: pi(s,a) > 0 -> u(s,a) > 0

Quindi la policy che impariamo può/deve essere deterministica, mentre la policy di comportamento deve essere stocastica.

Predizione: Regole di update dei metodi di predizione off-policy:

Viene suggerito di non considerare il metodo off-policy con MC in quanto, per via dei troppi stati da esplorare nell'episodio, viene generata troppa varianza dei valori, il che rende la formula molto complicata.

Invece il metodo off-polcy funziona bene con il temporal difference, in quanto il rapporto tra u (mu) e pi risulta essere un rapporto tra probabilità il che non presenta il difetto della varianza.

Predizine + miglioramento dei metodi off-policy

Controllo MC

Nonostante MC non sia forse il metodo migliore nell'ambito degli off-policy, l'algoritmo cmq esiste, ne riporto lo pseudo codice sotto:

Questo algoritmo nel 2019 ancora non era stato ben esplorato, per cui per in questo corso non verrà approfondito.

Controllo TD

Quando si lavora con i metodi on-policy, viene utilizzata la stessa policy per esplorare gli stati e la si faceva migliorare e tende ad essere la policy ottimale. Si era poi deciso che per mantere una policy che sia in grado, da un lato di migliorare in maniera greedy e che nel contempo possa anche eplorare, di utilizzare le epsilon-greedy ovvero che facesse anche dell'esplorazione mentre migliora. 

A questo punto separiamo le due policy, ovvero scegliamo una poloicy che esplora e usiamo l'esperienza fatta con questa per aggiornare un'altra policy, che è quella che piano piano diventa migliore e che a questo punto può essere totalmente greedy. 

Il rapporto tra le due policy si chiama "rapporto di verosimilianza". Quando il rapporto tra i due è grande (pi/u) 

Controllo Q-learning

I Q-learning sono una famiglia di algoritmi, dove l'azione nel target la scelgo con la policy pi di improvement.

che migliorata si può scrivere:

dove la policy pi è scelta come max di Q ovvero in maniera greedy, mentre le altre azioni sono scelte con la policy "mu" esplorativa.

Nella pratica l'azione A viene scelta in maniera epsilo-greedy con la policu "mu" 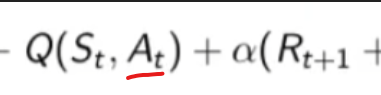   mentre l'azione dello stato di arrivo St+1 è scelta con la polict greedy  

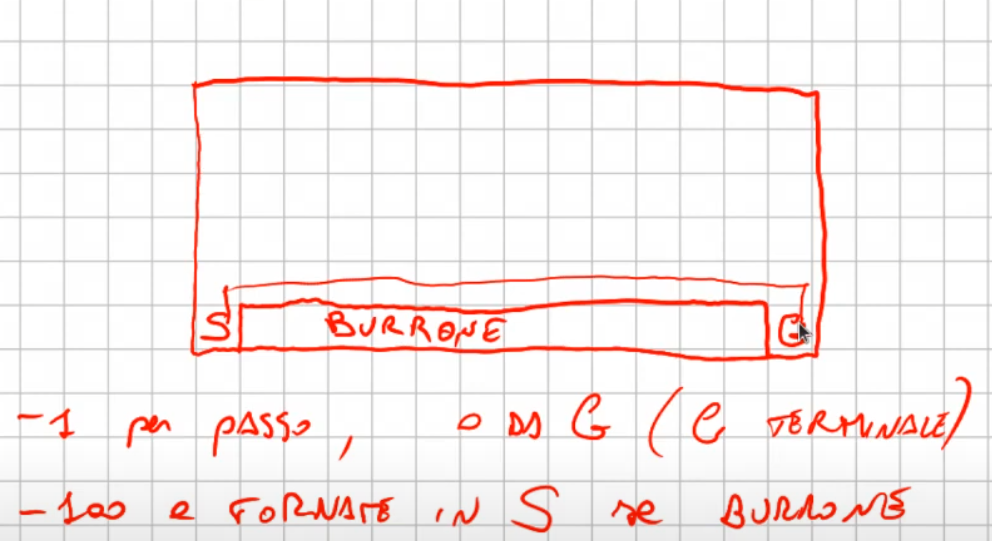
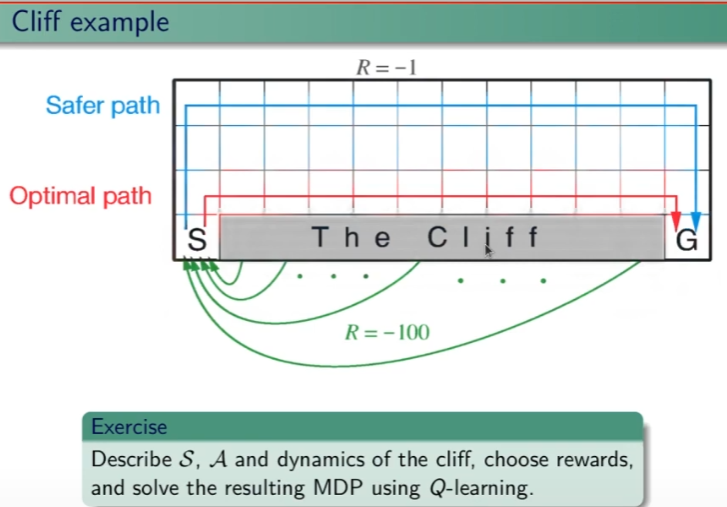
Ippotizziamo ora questo esercizio, ovvero un mondo griglia con un burrone come sotto riportato:

Vogliamo applicare l'algoritmo Sarsa e l'algoritmo Q-Learning. Sarsa è epsilo-greedy mentre Q-Learning è greedy. Quanto emerge viene riportato sotto:

ovvero che Sarsa (blu) trova un percorso sub-ottimale, questo perchè essendo epsilong-greedy, tende a "rischiare" di meno e quindi sbagliare di meno. Mentre invece Q-learning è si ottimale, ma tende a rischiare di più. Q-Learning è quindi meglio? Dipende, se abbiamo a che fare con delle simultazioni, allora è sicuramente meglio, se invece abbiamo a che fare con il mondo reale dove i rischi sono reali allora è meglio scegliere una soluzione più "safe" come quella di Sarsa.

Se quindi misuro la somma delle ricompense il Q-learning ne riceve meno in quanto appunto rischia di più in quanto, nell'esempio tende a cadere maggiormente nel burrone. (vedi gradico sotto riportato)

Miglioramento della policy target pi Q-Learning (detto Sarsa Atteso o Expeted)

Target Q-Learning (predizione ovvero fissato pi) -> R + gamma*Q(S',A') dove A' è campionata di pi di S' che si scrive (A=pi(.|S')

ovvero:

questo algoritmo migliora il Sarsa On-policy e il Q-Learning Off-policy.

Questo è un metodo che stima il modello, lo impara e lo usa man mano che lo imparano, sono detti "model based".