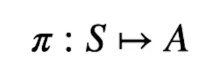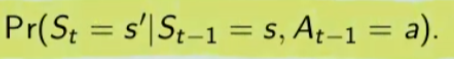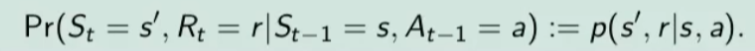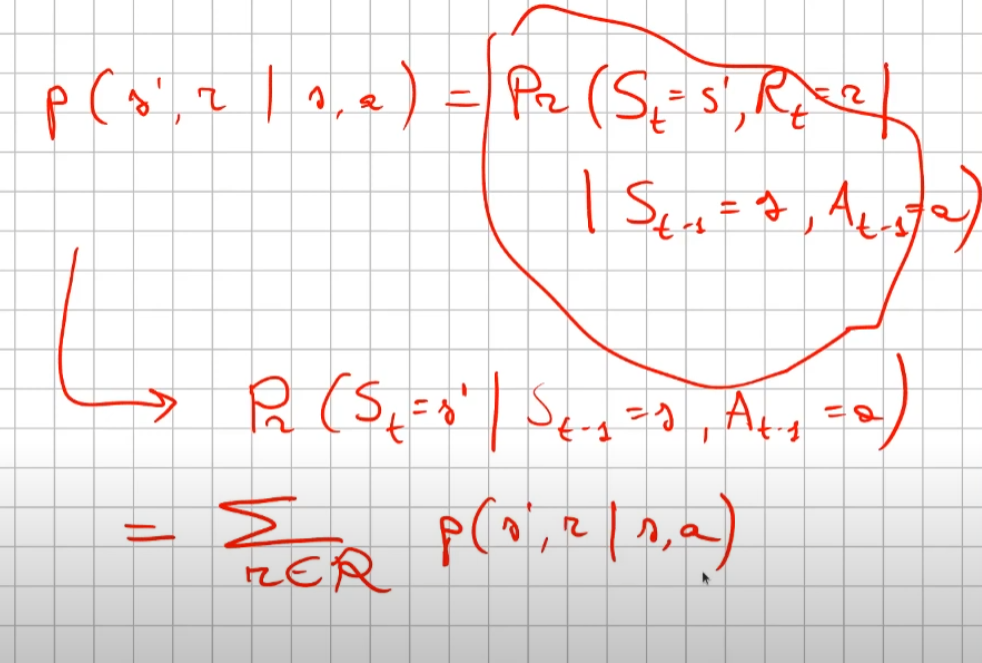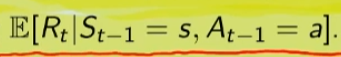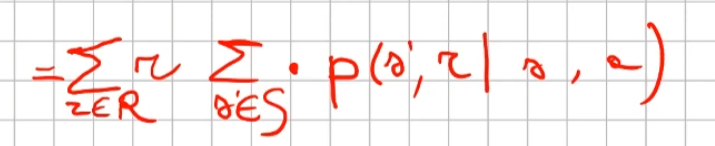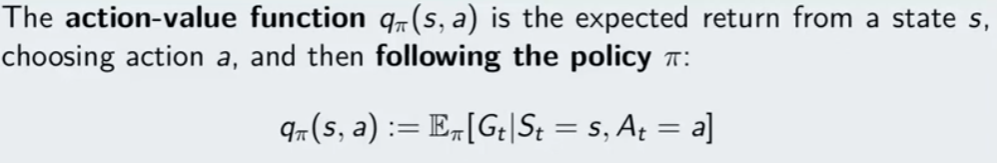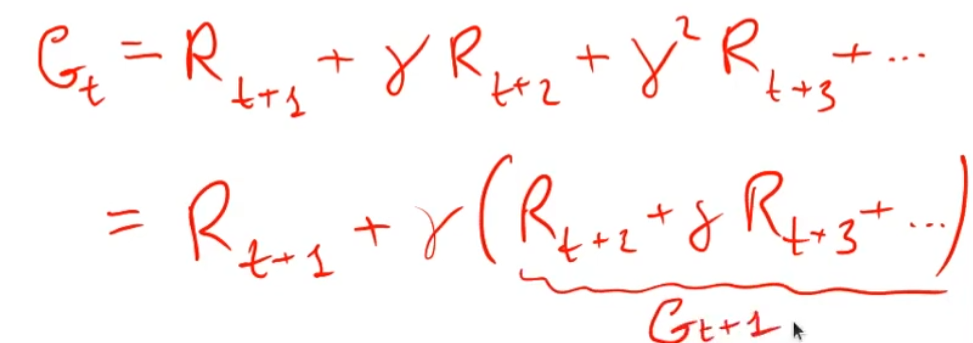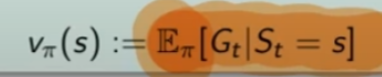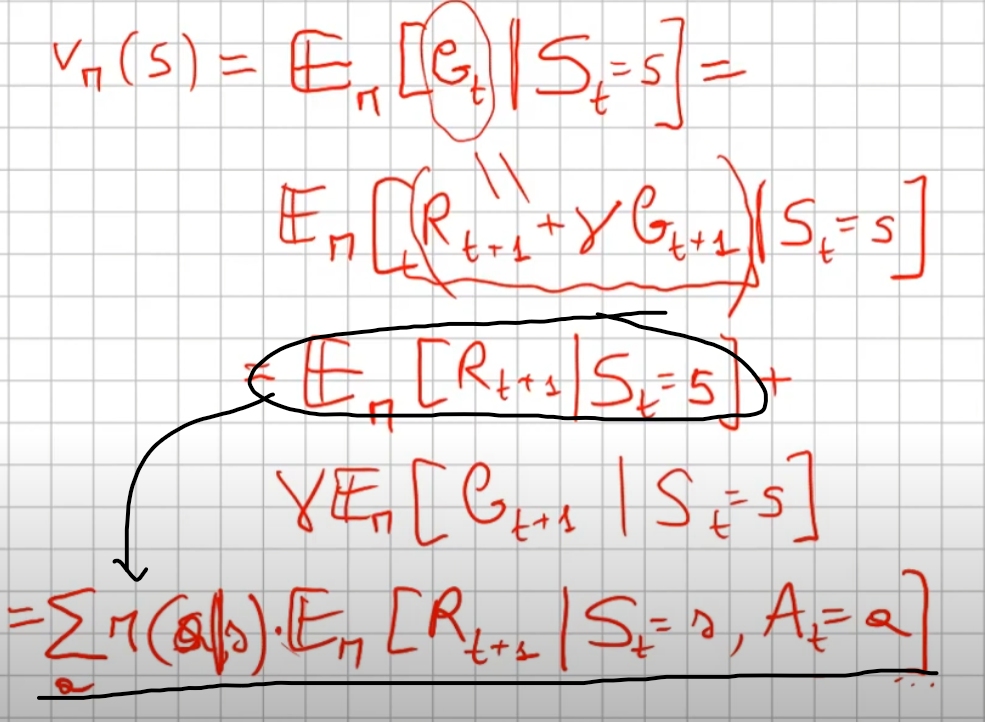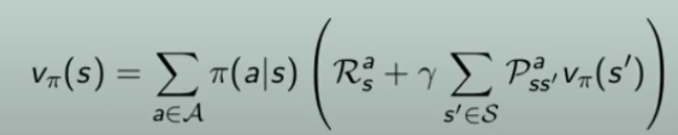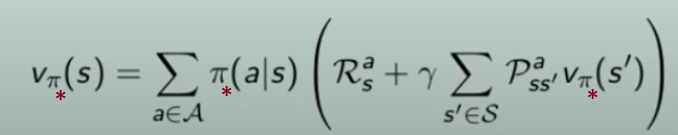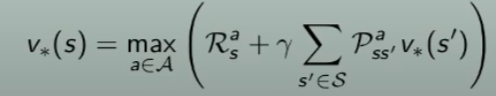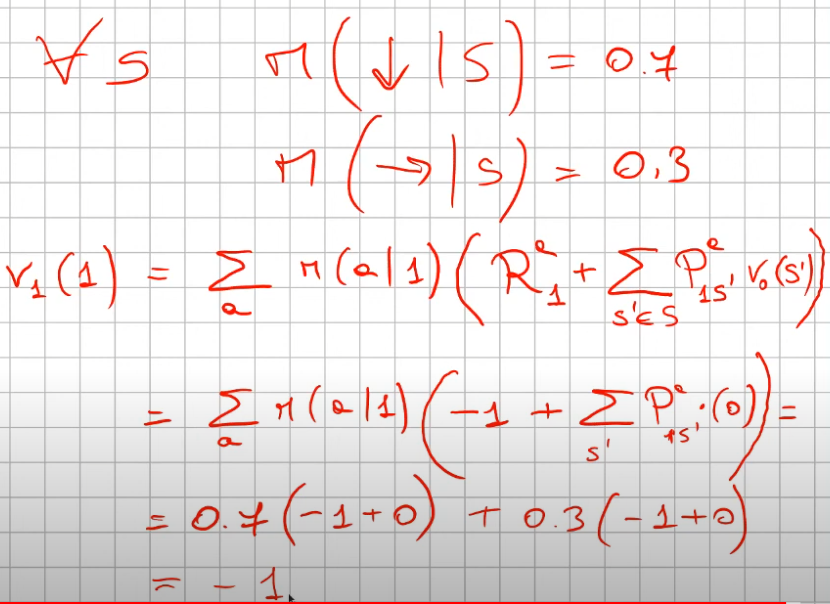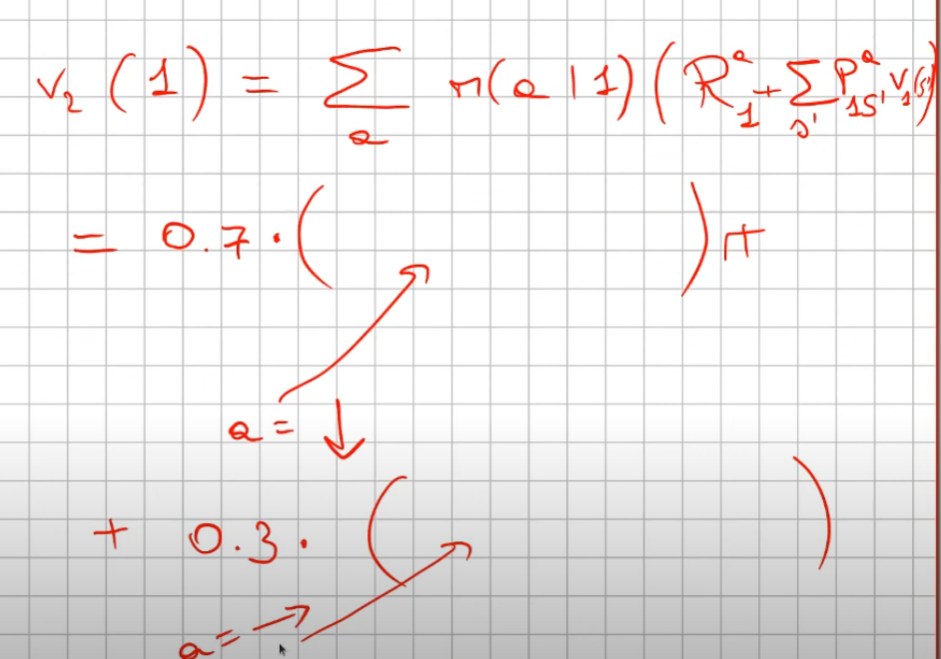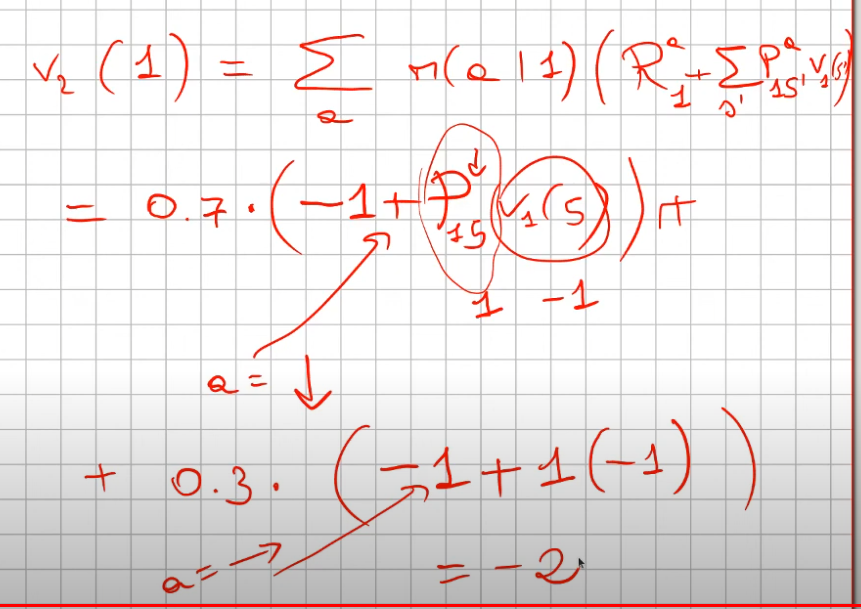Sessione 1

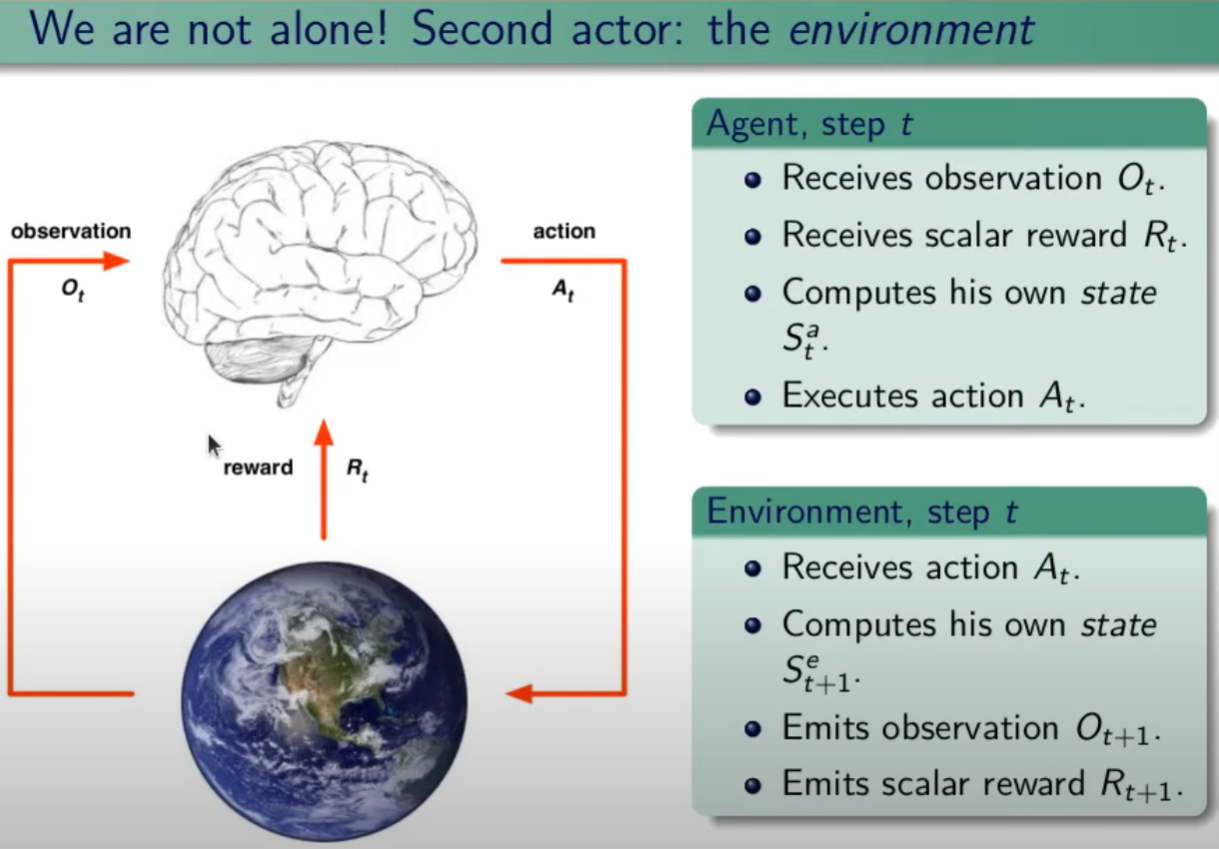
Nell'apprendimento per rinforzo (d'ora in poi verrà indicato con RL) si basa sul processo decisionale di Markov aka MDP attrraverso un task di controllo dove un set di possibili stati e azioni ritornano un reward e una probabilità di passaggio ad uno stato all'altro. Il task nella pratica è un "compito" o una simulazione che per essere svolta (risolta) implica l'utilizzo dell'MDP.

NB: Il processo decisionale di Markov (MDP) asserisce che il passaggio allo stato successivo T+1, dipende esclusivamente dallo stato attuale T e non dagli stati precedenti. Quindi il processo NON ha memoria, in questo caso si dice che il processo è "Markoviano".

Tipologie di processi decisionali di Markov (MDP)

Esistono due tipologie di MPD, il processo a stati finiti e quello a stati infiniti.

Nel MDP finiti gli stati finiti hanno un numero finiti di stati definiti dall'ambiente, es. l'uscita da un labirinto di 5 caselle x 5. In questo caso abbiamo 25 stati e 4 azioni (su, giù, dx e sx)

Nel MDP a stati infiniti, invece, l'ambiente appunto può restituire infiniti stati a fronte di infinite azioni, pensiamo per es. il sistema di guida automatica di una macchina dove l'azione es. girare il volante, è un valore continuo così come la scelta della velocità dell'auto.

Episodi

MDP definisce anche degli "episodi" in particolare:

Nel MDP episodico un episodio termina a determinate condizioni. Es. nel gioco degli scacchi quando la giocare da scacco matto.

Nel MDP continuo, il processo non ha fine, semplicemente continua ad esistere all'infinito in quanto non esiste uno stato fine.

Traiettoria ed episodio

La traiettoria è il movimento che l'agente compie per muoversi da uno stato all'altro. La traiettoria è definita dal simbolo greco 𝜏 "tau". Un esempio può essere:

𝜏 = S0, A0, R1, S1,.A1, R2, S2, A2, R3, S3 che indica la partenza dallo stato zero, dove viene effettuata l'azione A0 che porta la reward R1 e il posizionamento nello stato S1, alla quale segue l'azione A1 e così via. L'ultimo stato della traiettoria sarà (nel caso specifico) S3.

La treittoria può essere finita o infinita, se è finita si chiama episodio è semplicemente una traiettoria che inizia in uno stato e finisce nello stato finale oltre quale non si torna indietro. es: 

= S0, A0, R1, S1,.A1, R2, S2, A2, R3, S3, ..... RT,ST.

di cui deriva il concetto di storia, ovvero la somatoria delle osservazioni, ricompense e azioni  fino all'azione finale.

Ricompensa vs Ritorno

La ricompensa (reward) viene restituita a fronte di un'azione, quindi per risolvere un task, dobbiamo massimizzare le ricompense ottenute. La ricompensa è quindi un risultato immediato. (Rt)

Invece il ritorno è la somma di tutte le ricompense ad un determinato momento nel tempo es: G(t) = R(t+1) + R(t+2) + ... R(T) finchè il task è stato completato.

Predizione, miglioramento e Controllo

La predizione significa calcolore il valore di una certa policy fissata,  il miglioramento, come dice la parola serve per migliorare (anche solo di poco, non la miglioare in assoluto)  la policy attuale, mentre il controllo serve per trovare la migliore di tutte.

Da qui il ciclo utile per trovare la policy migliore: pi(s) -> Vpi(s) -> pi'>= pi che inserire in un loop fino a quando converge. (teorema banach caccioppoli)

Fattore di sconto γ (gamma)

Il fattore di sconto è un incentivo per completare l'episodio nel miglior modo (più efficiente) possibile. Per ottenere questo la ricompensa dovrà essere moltiplicata per il fattore di sconto che diminuirà nel tempo all'aumentare delle azioni intraprese, rendendo le ricompense sempre più basse e quindi disincentivando le traiettorie lunghe.

Il fattore è un valore compreso tra zero e uno e viene elevato ad un esponente corrispondente dall'iesima azione fino alla fine dell'episodio.

Se γ (gamma) vale zero l'agente cercherà di prendere una ricompensa immediata, il che denota una strategia miope che non ottimizza l'apprendimento. Al contrario invece, un fattore γ gamma pari a uno, rende l'agente più "paziente" e quindi non prono ad ottimizzare gli step dell'episodio. In genere il fattore gamma viene settato a 0,99 che forza l'agente ad avere una ricompensa immediata ma allo stesso tempo lo forza ad avere una visione "a lungo termine". 

In conclusione il fattore gamma indica all'agente quanto può valutare in maniera ottimali le azioni future.

NB: se il task è episodico allora è possibile utilizzare un fattore di sconto pari a 1, diversamente se il task è continuo (infinito senza stati assorbenti terminali) allora il tasso di sconto è meglio che sia <1.

Policy

La policy dell'agente è una funzione che prende in input uno stato e ritorna l'azione che va presa in quello stato. E' rappresenta dalla lettere greca pigreco π

La probabilità di eseguire un'azione (a) nello stato (s) si può rappresentare come:π(a|s)

L'azione che la policy sceglie nello stato (s) viene descritta dalla formula: π(s)

Dipende quindi dal contesto, in alcuni casi si uitilzza il primo π(a|S)  in altri il secondo π(s).

La policy può essere di due tipi: stocastica o deterministica.

Si dice che la policy è deterministica quando viene scelta sempre la stessa azione in un determinato stato quindi stiamo parlando del caso π(S).

Si dice invece stocastica quando l'azione viene scelta sulla base delle probabilità es. : π(S) = [0.3, 0.2, 0.5] ovvero la probabilità di effettuare una azione nello stato S, è del 30% nel primo caso, 20% nel secondo e 50% nel terzo. Quindi siamo in presenza del caso π (a|S)

Quindi bisogna trovare la policy ottimale rappresentata come π* (pigreco - asterisco) che sceglie le azioni che massimizzano la somma dei fattori di sconto per le ricompense alla lunga.

La policy π è una distribuzione di probabilità che deciamo noi dato lo stato con la quale scegliamo le azioni e prendendo quindi una decisione, si differenzia dalla probabilità che NON decidiamo noi che si rappresenta con P che invece rappresenta il modello la cui prabobilità non possiamo modificare. (es. P(s',r|s,a) )

Il valore della policy V in genere indica la ricompensa totale media che si ottiene applicando la policy

Controllo Ottimale

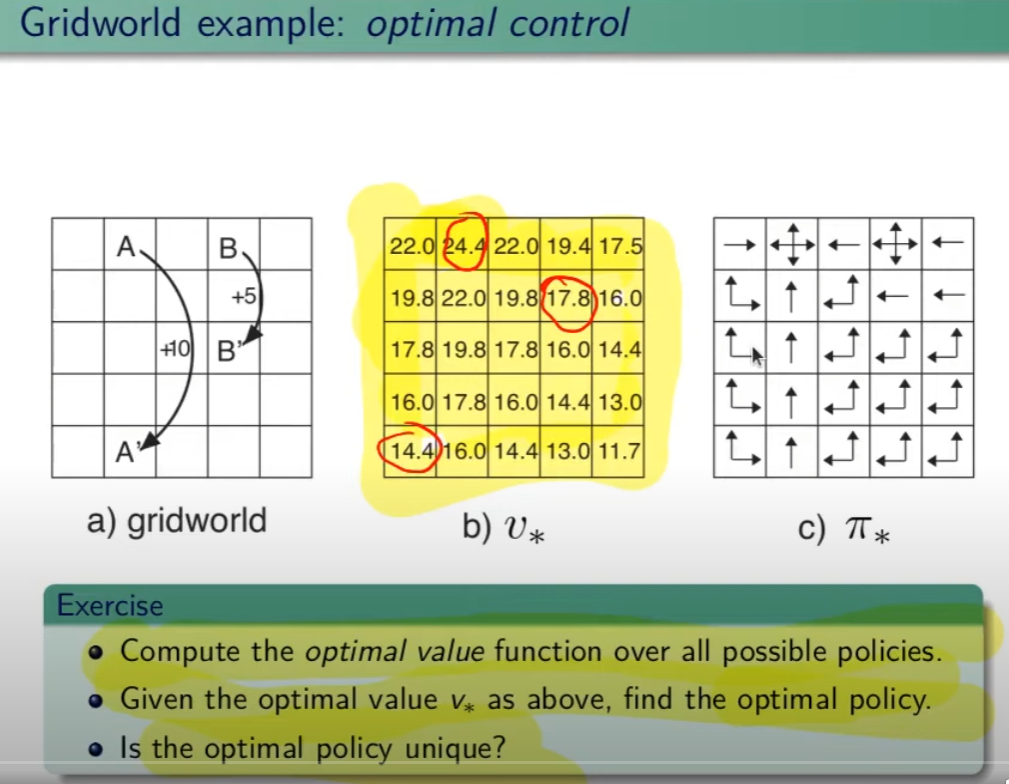
Nel RL è fondamentale determinare la Policy Ottimale π* indispensabile per la gestione dell'ambiente. La griglia di centro (visibile in figura) è la rappresentazione del valore di ciascuno stato. (dove per stato si intende ogni casella della griglia) Per valore ottimale V* si intende il valore della policy ottimale, ovvero quello che si può ottenere facendo le azioni migliori possibili. Per migliore azione si intende determinare lo scopo, ovvero massimizzare le somma delle ricompense (dette ritorno) ottenibili con le azioni future. 

La policy ottimale quindi, si ottiene valutando di volta in volta il valore ottimale. Le policy ottimali sono tante, anche su un unico stato, vedi per es. che nella casella in fondo a sx il cui valore è 14,4 ha due policy ottimali in quanto i valori ottimali in questo specifico caso sono due.

Pianificazione e Apprendimento

L'apprendimento nel RL si basa sulla pianificazione.

La pianficazione implica la conoscenza del modello associato all'ambiente, es. il lancio di un dado che implica che il valore medio detto anche ritorno medio dell'azione è 3,5 ovvero 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6.

NB: il modello è l'ambiente e normalmente NON lo conosciamo.

L'apprendimento, è la fase successiva alla pianificazione e implica l'iterazione con l'ambiente e prevede il calcolo della media empirica  ovvero la media dei valori ottenuti dall'iterazione con l'ambiente.

Quindi con la pianficazione e l'apprendimento, l'agente migliora la policy.

Entrambi guardano avanti nel futuro calcolando i valori cercando il miglioramento della policy.

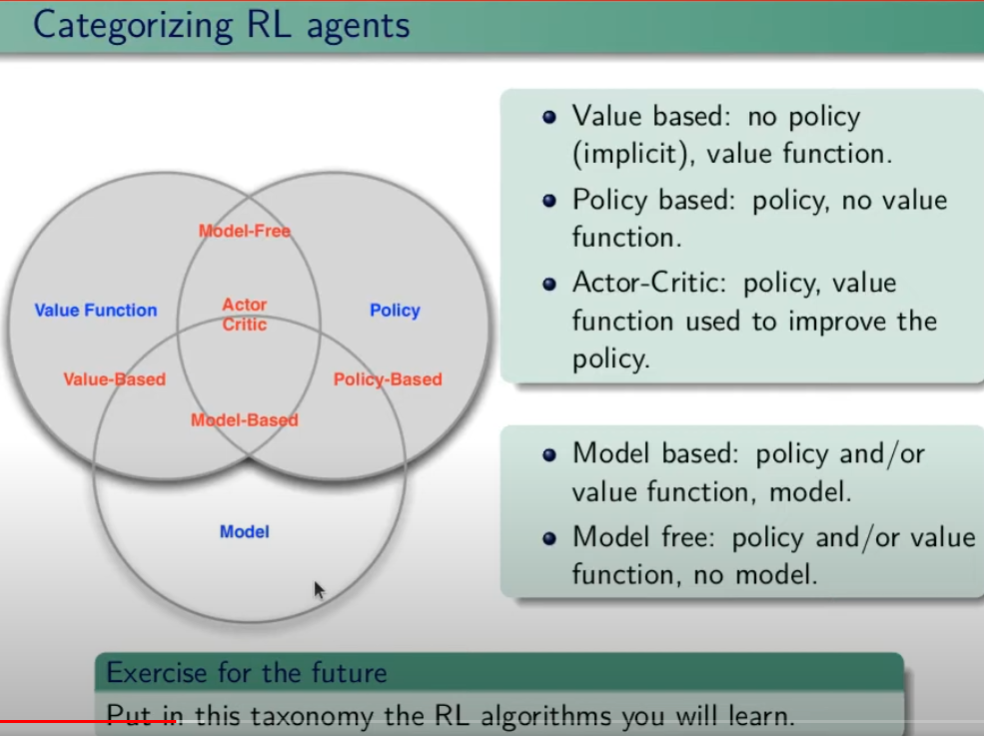
Tipologie di algoritmi applicabili al RL

Di seguito viene rappresentata la tassonomia (categorizzazione) delle varie tipologie di algoritmi applicabili nell'ambito del RL.

Esplorazione vs Sfruttamento

E' l'eterno dilemma, ovvero provo sempre nuove soluzioni o sfrutto sempre quelle che già conosco.  Entrambi vanno utilizzati per "allenare" la rete rete neurale. (vedremo più avanti)

Processi decisionali di Markov (MDP)

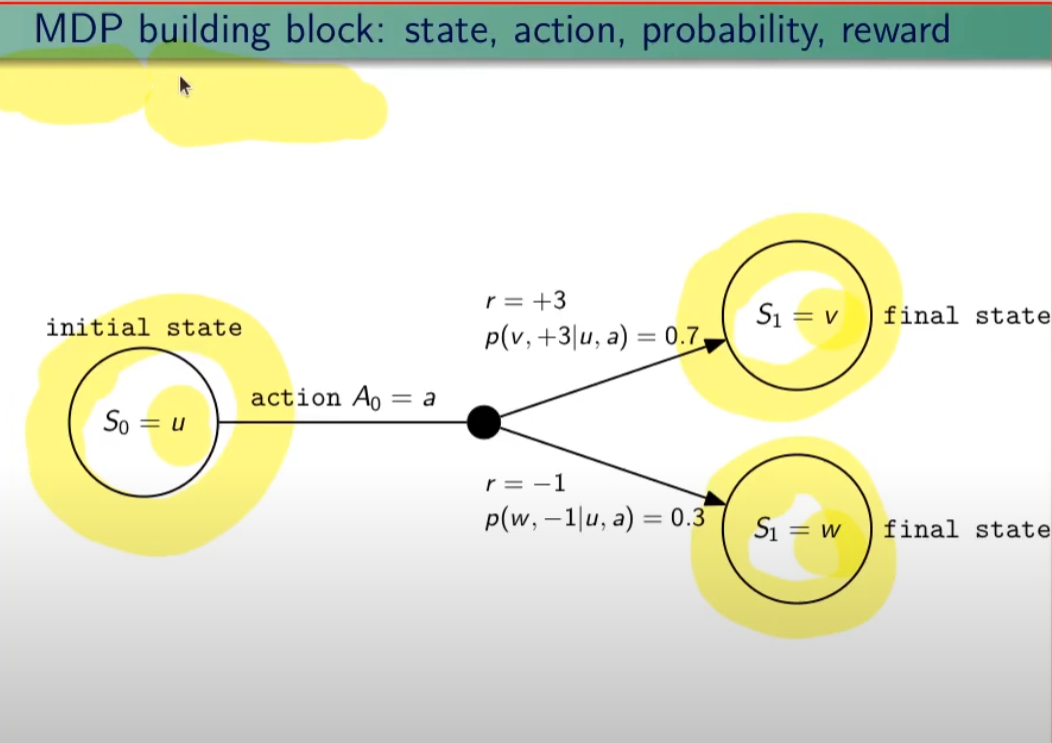
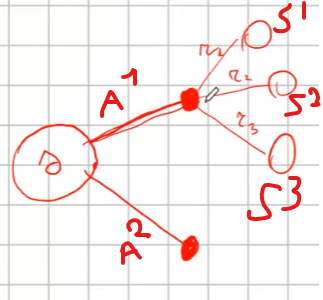
I processi decisionali di Markov si basano sulla gestione degli stati. Gli stati vengono rappresentati come dei cerchi dove all'interno è presente una lettera che lo rappresenta. Il pallino nero invece è l'azione.

Nello schema sotto rappresentato vediamo che, partendo dallo stato "u", la risposta dell'ambiente a fronte dell'azione "a" di tipo probabilistico (aleatoria) e quindi non deterministico, è di 0,7 con un reward di +3 che ci porta di v, oppure 0,3 con reward -1 che ci porta in "w". Se invece a fronte di una azione (pallino) ci fosse stato una unica determinazone della riposta dello stato T+1 anzichè due o piu, allora la risposta sarebbe stata derministica.

Es. leggendo la risposta dell'ambiente a fronte dell'azione a (nel caso dello 0,7 - 70%) è: la probabilità di arrivare in "v" con una ricompensa di +3, dato che sono partito dallo stato iniziale "u" e ho fatto l'azione "a".

Sempre rimandendo nel diagramma sopra riportato, qual'è la probabilità di andare in "w" con una reward di 42? (vedi figura sotto)

La risposta è zero in quando deve verificarsi la combinazione stato + reward che in questo caso non esistendo è quindi pari zero.

NOTA: lo stato terminale si indica con un quadrato.

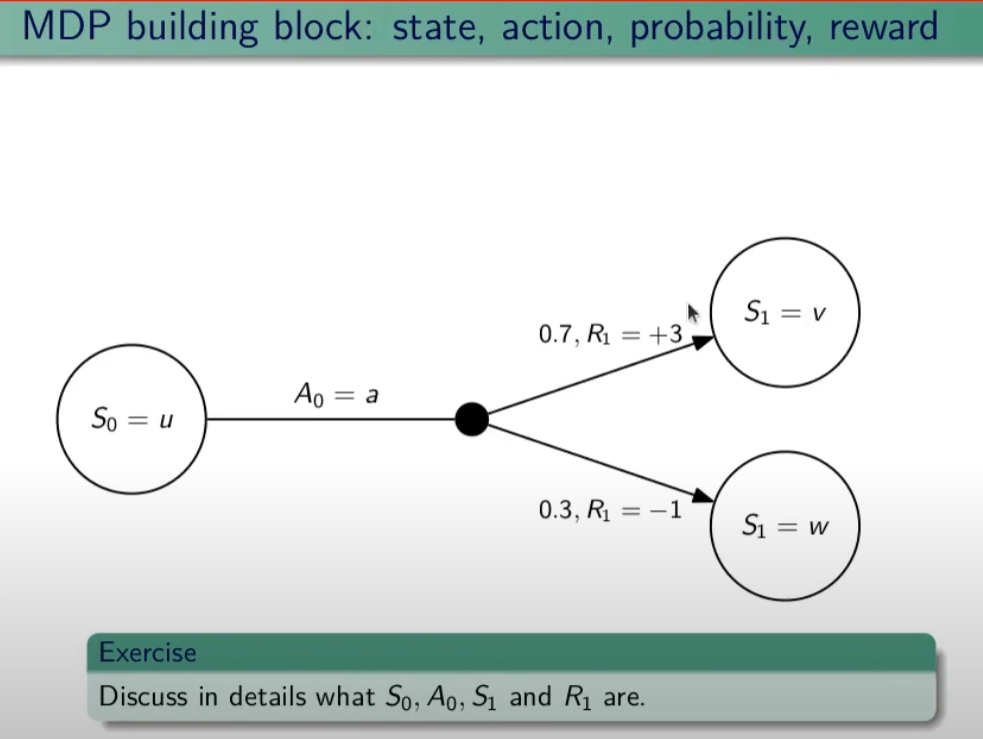
Ora semplifichiamo un attimo lo schema per renderlo più leggibile come sotto riportato:

Nello specifico la differenza tra S0 e S1 indica la situazione dello stato "S" al tempo T. Ovvero S0 è lo stato iniziale, mentre S1 è sempre lo stato S ma al tempo T+1 e può valere "w" o "v" a seconda della probabilità. Se ci fosse uno stato successivo S2 dovremmo considerare le probabilità di transizione da S0 a S1 e da S1 a S2.

La rappresentazione è quindi un grafo orientato in quanto unidirezionale. i tondi sono le azioni e gli archi i risultati probabilistici delle azioni.  

Ho quindi un insieme di stati S e di azioni A e di rewards R. Dopo ogni azione ho quindi una distribuzione di probabilità su SxR. Per ogni coppia di stato azione ho una distribuzione di probabilità. Conoscere il modello significa quindi conoscere la distribuzione di probabilità. Introduciamo anche il fattore di sconto gamma che vale sempre di meno all'allungarsi della distanza di tempo in modo che l'agente sia incentivato a trovare la soluzione migliore più velocemente.

La funzione p rappresenta quindi il modello, è quindi la probabilità di transizione dallo stato al tempo T-1 allo stato al tempo T. (a fronte di una certa azioen e relativa ricompensa)

Generalizzando quanto sinora detto:

dove il simbolo ｜ (pipe) indica che un elmento "a"  è condizionato da "b",  es. "a | b". Occhio che per es. P(a,b) è la probabilità dato in input "a" e "b" mentre invece P(a|b) significa la probabilità dato "a" e condizionato a "b" MA "a" puà assumere più valori in B.

dove il simbolo ~ (tilde) indica che uno stato S è preso da una certa distribuzione di probabibilità P, es. S ~ P(...) 

Esercizio:

nota: ricordare che il simbolo 𝔼 rappresenta il ritorno atteso ovvero il valor medio dei ritorni.

In pratica 𝔼 rappresenta il valore medio (media dei valori pesati) delle ricompense che posso ottenere in un determinato stato S. Questo perchè in uno stato protrei avere una distribuzione di probabilità che per es. a fronte di una azione possono scaturire più azioni con associata una proababilità e un ricompensa ciascuna. es: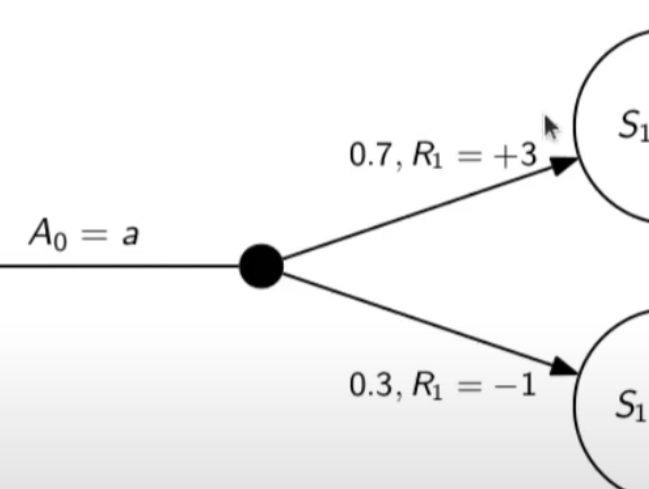  

1)

La prima riga si legge così: la probabilità che un stato S al tempo T sia s' condizionato al  fatto che lo stato precedente fosse s e che io abbia fatto precendetemente una derminazione azione a. Quindi si vuole sapere la probabilità di essere nello stato s' nel caso in cui nello stato precedente s sia stata eseguita l'azione a.

Per ricavare questa probabilità bisogna partire la formula generica MDP che tiene conto delle rewards, ovvero:

quindi per rispondere al prima quesito dobbiamo sommare tutte le rewards in modo che rimanga la sola probabilità che ci porta allo stato s', in quanto non vogliamo la probabilità che esca s' e r, ma vogliamo solo la probabilità che esca s', oovero:

perchè sommando tutte le rewards ho la certezza di finire nello stato s'. Sommare tutti gli "r" si dice anche saturare tutti gli indici r.

2)

In questo caso invece si desiderata la ricompensa media (variabile aletoria) al tempo "t" condizionata dal fatto che al tempo t-1 partissi dallo stato "s" e facessi l'azione "a".

Quindi il valore medio della ricompensa sarà la sommatoria di tutte le ricompense ciascuna di esse moltiplicate per la propria probabilità di uscita, ovvero:

dato che in questo caso vogliamo la reward media al tempo  t, come nel caso 1) dobbiamo "saturare" un fattore, in questo caso sono gli stati. Quindi per tutti gli stati s' moltiplichiamo la probabilità ritornata dall'azione a nello stato "s" a t-1 per tutte le reward. La prima sommatoria estrare tutte le reward che vanno a moltiplicare le corrispittive probabilità. Moltiplicando reward per la probabilità si ottinene la reward media. (vedi esempio del valotre medio del lancio del dado, dato dalla sommatoria del valore di ciacuna faccia del dado per 1/6 per un totale di 3,5)

3) per ora non viene spiegato.

Dinamica del MDP: rappresentazione tabbellare

Una delle tecniche più basiche di rappresentazione delle transizioni da uno stato all'altro fa uso di matrici di valori che indicano la probabilità di transizione da uno stato all'altro. Se per esempio un sistema ha 4 stati, la tabella sarò composta da una mtrice di 4x4. Ovviamente questo metodo funziona con sistemi i cui stati sono molto limitati, non per funziona con sistemi complessi come per es. gli scacchi o la dama.

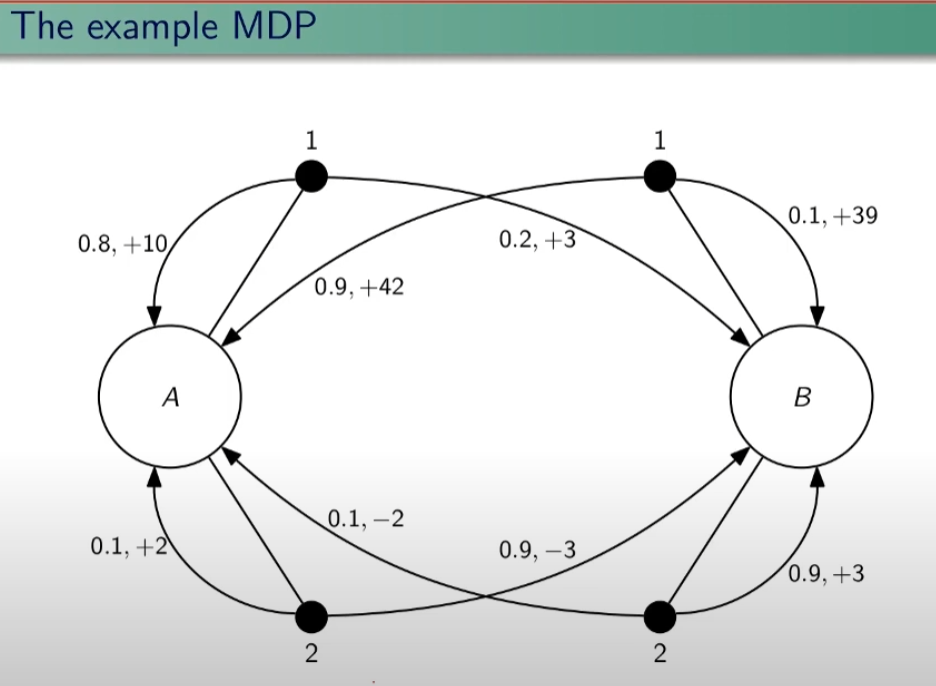
Facciamo un esempio, calcoliamo su questo MDP delle quantità:

Iniziamo con il calcolo di una matrice di transizione detta matrice stocastica, in queso caso avendo due stati la matrice è 2x2, nelle celle della matrice andremo ad inserire le probabilità di transizione da uno stato all'altro. Nell'esempio sotto riportato andremo a calcolare la matrice associata all'azione 1. La peculiarità di questa matrice è che la somma di ciascuna riga da sempre 1 - 100%.

P = 1 (azione 1)	A	B
A	0,8	0,2
B	0,9	0,1

Calcoliamo ora il vattore ricompensa associata all'azione 1.

R = 1 (azione 1)

10*0,8 + 3*0,2 = 8,6

0,9*42+0,1*39 = 41,7

ora creiamo che tabella che rappresenta l'intero modello:

s (stato partenza)	a (azione)	s' (stato di arrivo)	r (ricompensa)	p(s',r | s,a) probabilità
A	1	B	3	0,2
...

La tabella conterrà un totale di righe dato dalle azioni x numero di probabilità di accedere allo stato, questo caso 8.

La proprietà di "Markovianità"

La proprità di markov indica che il valore dello stato St dipende esclusivamente dallo St-1 ma non dipende dagli stati precedenti a St-1. (es. St-2, St-3 etc etc)

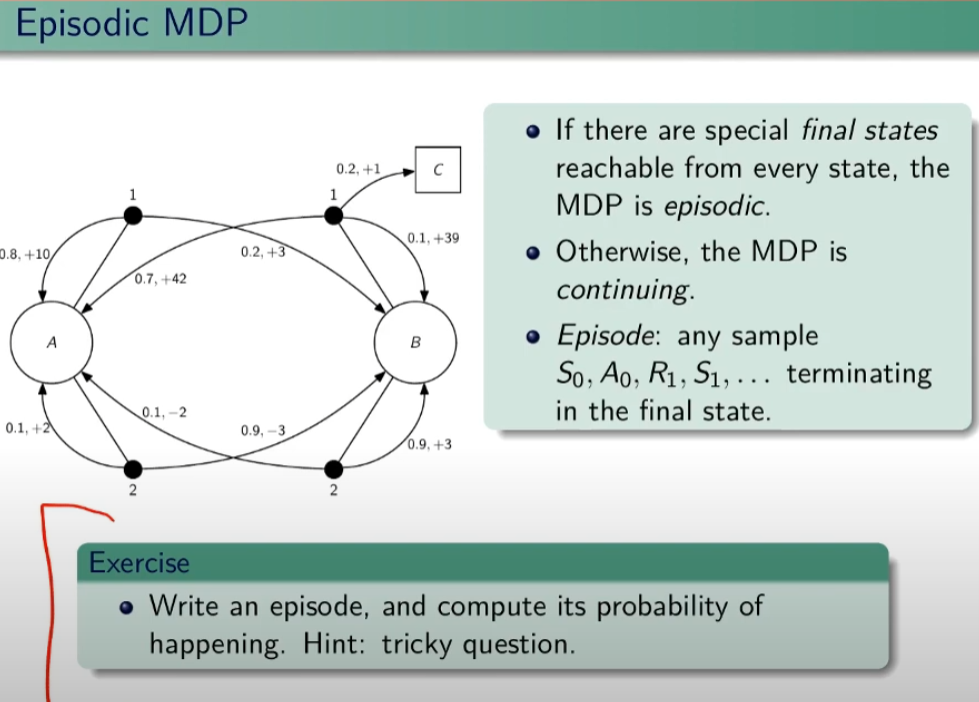
Episodi MDP

Se ho uno stato terminale tra gli stati possibili allora il mio task si chiama episodico. Attenzione che però dipende dalla policy, ovvero se ho delle azioni che mi consentono di evitare lo stato terminali posso entrare in loop. E' compito dell'algoritmo evitare questi loop. Nel caso in cui non esista lo stato terminale si tratta di un MDP continuing.

Esiston anche task a orizzonte temporale definito se esistono dei limiti temporali.

Un episodio quindi è una sequenza di stati, azioni, rewards che terminano con lo stato terminale.

Simuliamo un episodio:

EPISODIO: A, 1,10, A, 2, -3, B, 2, 0,9, B , 1, 1, C

PROBABILITA': dipende da:

• probabilità di scegliere (1|A)
• probabilità di scegliere (2|A)
• probabilità di scegliere (1|B)
• probabilità di scegliere (2|B)

Per calcolare un episodio bisogna capire quindi come viene definita la policy.

Un esempio di policy π  che per esempio può essere scegliere sempre l'azione 1. Quindi la policy "pi" è fondamentalmente una strategia che può (e spesso deve) variare per massimizzare il ritorno.

Ritorno

Il ritorno (G = gain) è la somma delle ricompense di un episodio ed è una variabile aleatoria.

NB: L'ipotesi è che i ritorni R abbiamo un limite superiore finito che consente al fattore di sconto far convergere il ritorno totale.

Ricordo la notazione che si ripeterà spesso nel corso, 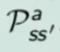  ovvero la probabilità che facendo un'azione "a" nello stato "s" l'ambiente mi porti nello stato s'. Il mio comportamento è rappresentato da una distribuzione di probabilità negli stati S. La strategia di scelta delle azioni - che sia chiama polocy - è una distribuzione di probabilità neglis stati.

Le policy ottimali possono essere deterministiche o non deterministiche. Un esempio di policy determinisca è il lancio de dado in quanto ho una sola possibile azione, appunto il lancio del dato, invece un esempio di non deterministica è per es. sasso-carta-forbice. 

Funzione stato-valore

La funzione stato valore per un MDP è il numero che ci indica quale azione intraprendere. Si rappresenta come:

dove V è il valore indicizzato dalla lettera pi (policy) indicizzato dallo stato S.

Mentre "E" è il valore atteso/valore medio, è il valore dello stato, è il numero teorico che se lo conoscessimo aprioristicamente ci "renderebbe la vita più semplice" in quanto significherebbe che conosceremmo l'ambiente, cosa ovviamente non possibile. (spesso il valore E è la media ponderata dei valori attesi)

"E" il è il valore che voglio massimizzare, viene quindi indicato con la lettera "V" che sta per valore indicizzato a pi-greco ovvero la "policy" cioè quello che facciamo noi espresso in probabilità di effettuare un'azione, dello stato "S" (notazione funzionale)  uguale al valore medio atteso di Gt -> ritorno al tempo "t" condizionato al stato "s" che è l'argomento della funzione Vπ( s)

Q-learning

E ora veniamo ad un concetto molto importante, il concetto del Q-learning, ovvero action value function che sta per qualità dell'azione.

Qπ(s,a) = rappresenta la qualità di una azione -> partedo dalla prima azione (fissata) e dallo stato (fissato) eseguo tutte le azioni che la policy mi dice di eseguire. Tenendo ovviamente in conto che il modello (P) mi dice quale sarà il nuovo stato e la ricompensa e la policy π deciderà quale sarà la nuova azione da eseguire.

Vπ(s) = rappresenta il valore dello stato "s" (stato di partenza) che si ottiene seguendo le azioni dettate dalla policy π tenendo conto che la scelta delle azioni è di tipo probabilitstico quindi in teoria sarebbe πP. ("P" si omette) Questo guardagno è una variabile aleatoria. L'intenzione è quello il avere il valor medio (la quantità) più grande possibile

V*(s) = è il valore medio massimo ottimale che si può ottenere su tutti i Vπ(s)  applicando tutte le policy possibili. -> maxπ Vπ(s)

Q*(s,a) =è la funzione valore ottimale -> maxπ qπ(s,a)

In fine definiamo la policy ottimale π* in grado di massimizzare il valori (sia l'azione valore che la stato valore)

Ora facciamo un esempio:

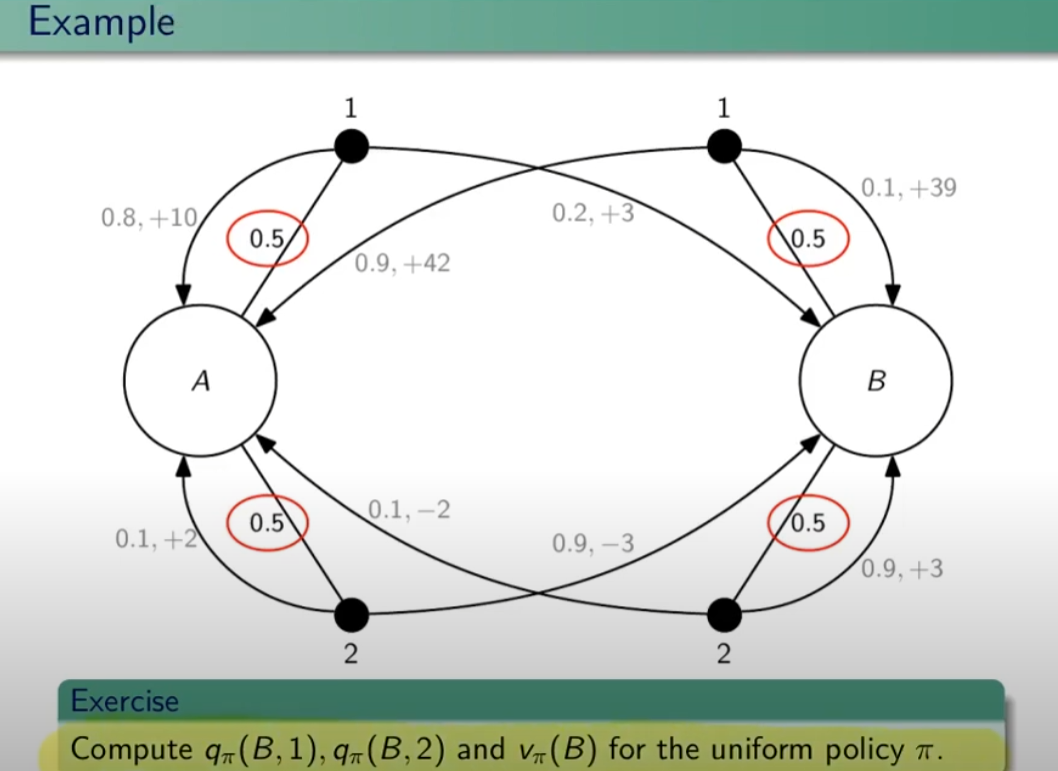
 Esercizio: calcolare il q-values applicando la policy pi nello stato B e compiendo l'azione 1 in un caso e l'azione 2 nell'altro; e calcolare il valore atteso nello stato B applicando la policy uniforme π.

Soluzione qπ(B,1)

qπi(B,1) = gamma*0,1*(39+ V_pi(B)) + gamma*0,9*(42+V_pi(A))

dove:

V_pi(B) = 0,5*q_pi(B,1)+0,5*q_pi(B,2)

V_pi(A) = 0,5*q_pi(A,1)+0,5*q_pi(A,2)

spiegone:

Per determinare la funzione q (valore azione) relativa alla policy π che nel caso di partenza  da B, è  necessario applicare la "policy di partenza" ovvero al 50% di probabilità di scegliere un'azione. Quindi la qπ(B,1) è calcolata come la probabilità di scegliere l'azione 1 (che in questo caso è del 100% in quanto viene impostato come richiesta iniziale) che moltiplica la probabilità del 10% di ottenere 39 sommato al valore-π dello stato di arrivo ovvero "B", più la probabilità del 90% di andare nello stato A ottenedo 42 sommato al valore-pi di A.

Il valore-pi di A è a sua volta la probabilità di scegliere l'azione 1 sommata alla probabilità di scegliere l'azione 2 ovvero: V_pi(A) = 0,5*q_pi(A,1)+0,5*q_pi(A,2).  (dove la probabilità per questa policy di scegliere l'azione è del 50%)

Analogamente il valore-pi di B è probabilità di scegliere l'azione 1 sommata alla probabilità di scegliere l'azione 2 ovvero: V_pi(B) = 0,5*q_pi(B,1)+0,5*q_pi(B,2). (dove la provabilità per questa policy di scegliere l'azione è del 50%)

Da notare che questa non è la policy ottimale in quanto è la policy di partenza che ci da il 50%, l'apprendimento sta nell'iterare il processo a fine di variare la % della policy per farla convergere a quella ottimale.

Bisogna quindi calcolare 4 equazioni con 4 incognite che sono: qπ(A,1) qπ(A,2) qπ(B,1) e qπ(B,2)

Per farla convergere però, bisogna utilizzare un fattore di sconto gamma, altrimenti tende a infinito... (di qui l'introduzione di gamma)

Questo ciclo (iterazione) viene anche detto controllo.

In conclusione questo sistema è una versione dell'equazione di Bellman.

NB: per ricompensa si intede la somma dei valori che il modello ci da quando da uno stato passa ad un altro. Quindi la ricompensa è composta da uno a più valori con relativa percentuale di ottenimento. (es. mi da valore 20 al 10%, valore 50 al 60% e così via) Una volta ottenuti tutti i valori dello stato si calcola il valore medio che appunto rappresnta la ricompensa.

Equazioni di Bellman

Ed eccoci ad uno dei capisaldi dell'apprendimento per riforzo, le equazioni di Bellman che si basano sui concetti sinora appresi, ovvero ritorno (somma delle ricompense), ricompensa, valore dello stato, funzione valore-azione.

Il ritorno Gt può essere formulato (descritto) in maniera ricorsiva in quanto è la somma delle ricompense.

Ovvero il ritorno al tempo t è la somma della ricompensa al tempo t+1 sommato al ritorno del tempo t+1, dove il ritorno al tempo t+1  è rispetto a t+1 (quindi es. t=2 scontato di gamma ovviamente)

dimostrazione:

quindi 

Gt = R(t+1) + gamma*G(t+1)

cvd

da qui ne deriva l'equazione di Bellman:

Funzione valore dello stato 

La prima equazione ricorsiva di Bellman

innanzitutto bisogna osservare che è un'equazione ricorsiva, in quanto all'interno della funzione è riproposta la funzione stessa.

Come si legge l'equazione di Bellman:

Partiamo dal presupposto che a questo livello stiamo pianificando, ovvero cerchiamo di capire cosa potrebbe accadere se faccessimo l'azione a1 piuttosto che l'a2.  In futuro vedremo come apprendere...

Quindi:

Partiamo dallo stato "s", abbiamo una policy π che ci fa scegliere ogni azione tra le azioni disponibili, con una certa probabilità, ovvero ->  

e quindi vediamo cosa succede, ovvero ->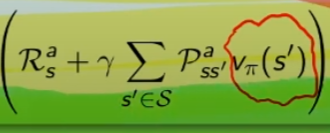  

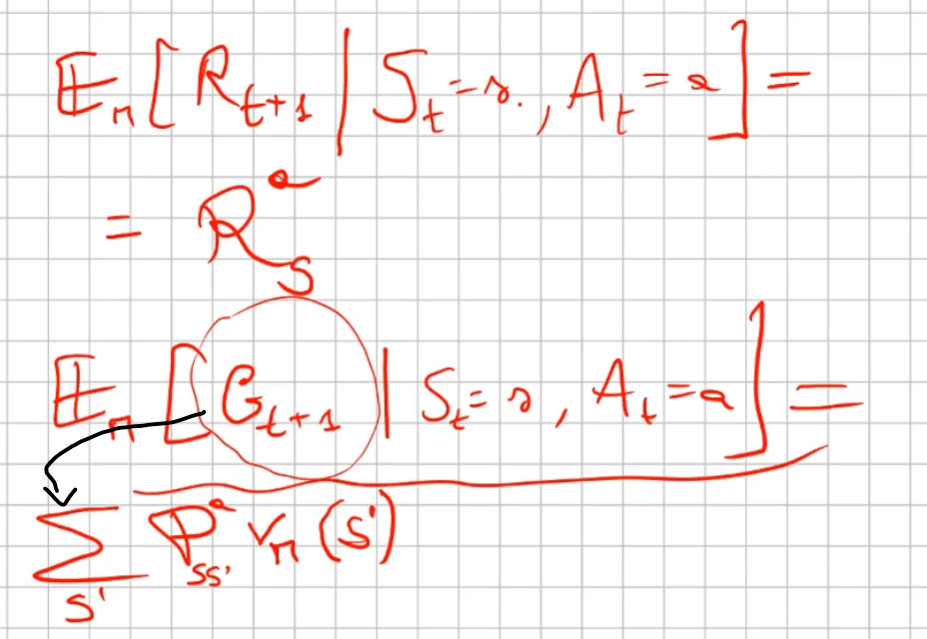
che significa: 

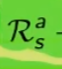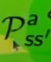la ricompensa media (è un singolo numero) ottenuta dallo stato "s" facendo l'azione "a"  sommata al valore dello stato s', la cui probabilità di arrivarci è data da   che rappresenta quindi la probabilità di passare dallo stato s a s', ed è una matrice di valori detta anche matrice di transizione.

dimostrazione:

partiamo dall'assunto:

che ci dice che il valore-pi allo stato S è pari al valore atteso dato dal ritorno al tempo t subordinato allo stato "s".

Vπ(S) = 

+

ovvero:

Funzione valore stato-azione

La seconda equazione ricorsiva di Bellman

Valori migliori possibili delle stati e delle azioni (policy ottimali V* e Q*)

Per migliorare la policy devo cercare il "meglio possibile" sia degli stati-valore che degli stati-valore-azione  nello stato s per tutte le policy possibili, e quindi sarà il valore più alto (max) ottenibile. Questi valori saranno indicati come V*(s) e Q*(s,a)

Però bisogna dire che le policy potrebbero essere infinite, quindi trovare il valore massimo di queste è un problema...

Tipologie di policy

Le policy possono essere:

1)  dipendenti dalla storia si chiama -> HD (history dependent)

2) dipendenti dal tempo e non dalla storia, si chiama -> MARKOV

3) se non dipende da nulla si dice "stazionaria" e si indica con pigrego (π)

Quindi nonostante l'insieme delle policy è un insieme infinito e quindi non è possibile trovare il massimo, allora come faccio? Bisogna quindi prendere un sottoinsieme di policy e in particolare quelle stazionarie e deterministiche, ma in che modo?

Possiamo farlo se agiamo su stati e azioni finiti. Le policy stazionarie e deterministiche sono tutte le possibili azioni associate agli stati. (che si rappressanta com A elevato alla S, dove A sono le azioni e le S sono gli stati)

Se esiste una policy "ottimale", cioè il valore di tutti gli stati è il valore V*/ Q* (massimo) di quello stato.

La policy ottimale è deterministica in quanto sceglie sempre l'azione (una) che massimizza il ritorno, come si trova? si trova agendo "greedy" sulle azioni.

quindi:

Equazione di ottimabilità per funzione stato valore ottimale V* di Bellman 

A questo punto troviamo l'equazione ottimale di Bellman per la policy π*

Partiamo dalla "classica" equazione di Bellman che agisce su tutte le policy, ovvero:

Modifichiamola facendola agire solo sulla policy ottimale:

V* = 

ma la policy valore ottimale sceglie le azioni in maniera greedy, quindi:

V* =  

da notare che la V* è ricorsiva in quanto compare all'interno della formula.

Equazione di ottimabilità per funzione azione-valore ottimale Q* di Bellman 

Ricapitolando, le equazioni di Bellman ottimali e non sono:

Risoluzione dell'equazione di Bellman

Partiamo dal presupposto che l'MDP è un processo finito, ciò significa che gli stati sono definiti e numerati. I metodi per risolvere l'equazione sono di tipo "iterativo".

NB: In questa fase non stiamo facendo ancora apprendimento, stiamo facendo quella che viene chiamata "pianificazione" in quanto conosciamo il modello. Per implementare la pianificazione, vengono utilizzate tecniche di programmazione dinamica.

La programmazione dinamica è una tecnica di risoluzione dei problemi, si applica in due fasi:

• il problema complesso viene scomposto in sotto-problemi più semplici
• i sotto-problemi vengono poi ricomposti per risolvere il problema originale

Ci sono però dei requisiti, ovvero:

• il problema deve poter essere scomposto, si dice in questo caso che deve avere "una sotto-struttura ottimale"
• i sotto-problemi devono essere sovrapponibili, ovvero alcuni calcoli si possono ripetere in quanto l'algoritmo riceve in input gli stessi valori, per cui in questi è possibile implementare delle ottimizzazioni per evitare l'utilizzo di computazionale, come per es. l'utilizzo di cache, o altro.

Per calcolare la funzione valore di un policy dobbiamo quindi applicare l'equazione di Bellman iterativamente

Programmazione dinamica parte 2 (fase di pianificazione non apprendimento)

Stiamo quindi cercando di risolvere la fantomatica equazione di Bellman per determinare il valore dello stato e/o dello stato ottimale. La tipologia di casi che stiamo affrontando vengono detti "tabellari" in quanto, avendo a che fare con stati finiti, possono essere rapprentati in una tabella con valori finiti.

Per casi più complicati si utilizzano i casi "non tabellari" utilizzando gli approssimatori, ovvero le rete neurali.

Veniamo al pseudo algoritmo che utilizza l'equazione di Bellman.

spiegone:

L'algoritmo inizializza il vettore V con dei valori casuali tranne l'ultimo stato che deve essere inizializzato a zero, Questo perchè l'algorimo è di tipo "bootstrap" ovvero utilizza i valori del vettore al tempo t1 per deteterminare i valori degli stati al tempo t2. Lo stato "finale" deve essere assorbente, ovvero dallo stato finale o si esce o fa ripartire il loop di convergenza.

Ma questa versione non si usa, di seguito la versione migliorata, che in pratica utilizza l'ultimo valore per aggiornare V in quanto l'assegnazione di V svviene nel ciclo più interno, vedi sotto:

in questo modo tutti gli stati succesivi al primo beneficiano di valori aggiornati degli stati precedenti.

  Esercizio:

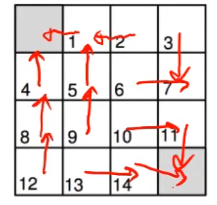
Di seguito abbiamo un "mondo griglia" con due stati finali.

Analisi:

gli stati sono 15, le azioni sono 4, un esempio di policy potrebbe essere: al 70% vado giù, e all'30% vado a destra.

Invece un esempio di policy ottimale:

Vedendo il modello possiamo pianificazione l'azione, per questo stiamo in modalità "pianificazione".

Ora proviamo con la policy: al 70% vado giù, e all'30% vado a destra.

Applicatione pratica dell'equazione di Bellman valore-stato (con policy non ottimale)

Policy Evaluetion

Ora veniamo al secondo passaggio, che va anche a spiegare il primo (rappresentato qui sopra)

Il secondo passaggio (v2) dopo che il primo passaggio  ha settatto il valore V degli stati a -1. (ad eccezione ovviamente degli stati finali T che valgono zero)

Il passaggio logico è:

La prima parte dell'espressizione è relatvia alla policy, che nel caso specifico è al 70% andare giù e al 30% andare a destra. (si legge come probabilità di raggiungere lo stato successivo s' facendo l'azione in s, dove s in questo caso vale 1 in quanto è lo stato 1)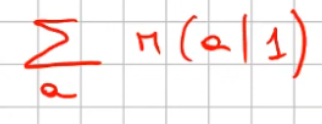 

Quindi  per prima cosa inseriamo nell'espressione le due probabilità 0.7 e 0.3 che moltiplicano una certa quantità.

 (questa quantità in formula si legge come la ricompensa media dell'andare nello stato s'  sommato alla probabilità dell'azione "a" di andare nello stato s' motiplicata (la probabilità) per la reward dello stato s'. Attenzione che la probabilità di anadare nello stato s' da s, in questo particolare caso, è 100% quindi 1. Da cui ne deriva che:

Il tutto va iterato per tutti gli stati dell'ambiente fino a che i valori degli stati "convergono", il che si significa che variano di poco.

Il metodo consente di propagare in modalità "backward" dagli stati finali (quelli più vicini allo stato T) verso quegli iniziali i valori.

Alla fine ciascuno stato del modello avrà un valore che indicherà quanti "passi" sono necessari per arrivare alla meta, dandoci quindi un'indicazione sul comportametno della policy.

Conclusioni dell'esercizio

Con una policy che assegna il 25% per ogni azione gli stati valori ottenuti sono:

[[  0. -14. -20. -22.]
 [-14. -18. -20. -20.]
 [-20. -20. -18. -14.]
 [-22. -20. -14.   0.]]

che indicano la ricompensa totale media che si otterrebbe partendo dallo stato. per es. se parto dallo stato "1" (quello vicino all'uscita) otterrei mediamente, con la policy al 25% una ricompensa media di circa -14.

ATTENZIONE! stiamo parlando di una ricompensa media in quanto ci potrebbero essere casi in cui arrivo subito all'uscita andando per es. subito a sx oppure casi in cui inizio a va girare per la griglia, esistono quindi traiettorie lunghissime.

Ecco l'esempio di codice:

allego a questa pagina le classi di ambiente utilizzate per simulare il "mondo griglia"

from envs.gridworld import GridworldEnv
import  numpy as np

# 0 su 1 dx 2 giù 3 sx
# instanzio l'ambiente griglia
env = GridworldEnv()


print (env.nS)
print (env.nA)
env.reset()
env._render()
env.step(1)
print()
env._render()
env.step(1)

def policy_evaluation(policy, env, discount_factor=1.0, theta=0.00000001):
    """

    :param policy: [A,S] matrice di shape (rango = 29  a due domensioni che rappresenta la policy, dove sulle riche ci sono gli stati e sulle colonne le azioni
    :param env: rappresentazione dell'ambiente
    :param discount_factor: fattore di sconto gamma
    :param theta: valore che termina la valutazione della policy una volta che la funzione stato valore è sotto questa soglia
    :return:
    """

    # inizializzamo la funzione stato valore V, per semplificare la vita li portiamo a zero
    # dove il valore è il valore di OGNI STATO
    V = np.zeros(env.nS)

    # il ciclo deve fermarsi solo quanto la qta delta calcolata è minuore o uguale a theta
    passaggi = 0
    while True:
        delta = 0
        passaggi += 1

        # per ciscuno stato effettuo un "full backup"
        # questo primo ciclo fa passare tutti gli stati
        for s in range(env.nS):
            v = 0

            # questo il ciclo fa la sommatoria delle azioni
            # ovvero esegue tutte le azioni possibili nello stato s
            for a, action_prob in enumerate(policy[s]):

                # per ciascuna azione chiedo all'ambiente in quale stato finisco, la probabilità di finirci, la ricompensa e se eventualmente è lo stato finale
                # NB: la situazione NON è vera in quanto stiamo facendo "esperienza" senza fare un passo, questo non è vero RL è pianificazione
                for prob, next_state, reward, done in env.P[s][a]:

                    # equazione di Bellman
                    # probabilità dell'azione per la probabilità della transizione
                    v += action_prob * prob * (reward + discount_factor * V[next_state])

            # quanto del valore stato funzione è variatto tra tutti gli stati
            delta = max(delta, np.abs(v - V[s]))
            V[s] = v

        # finiamo la valutazione una volta che il valore è sotto la soglia theta
        if delta < theta:
            break

    return np.array(V), passaggi

# definiamo una polcy generica, in pratica per ogni stato del mondo griglia associo 4 probabilità di eseguire una azione, le probabilità sono tutte al 25%
random_policy = np.ones( [env.nS, env.nA])/env.nA

v,passaggi = policy_evaluation(random_policy, env)

v = v.reshape(4,4)
print(v,passaggi)

Migliorare la policy (policy improvement-iteration)

Il metodo per migliorare la policy è quello di compiere tutte le azioni possibili e scegliere quella che restituisce il valore maggiore agendo in maniera "greedy", ovvero:

Come faccio a calcolare pi' (primo) ? be faccio tutte le azioni "a" possibili, faccio "one step looking forward", ovvero faccio un passo avanti compiendo un'azione sola, guardo cosa succede al passo successivo chiedento all'ambiente cosa può succedere con quale probabilità. Facendo queste azioni prendo quella che massimizza il ritorno.

Ma quando una policy è migliore di un'altra? beh quando per ogni stato s, applicando la nuova policy π', il valore dello stato è maggiore-uguale al valore della vecchia policy. Nella pratica  faccio N iterazioni compiendo N traiettorie fino a quando i valori convergano, a questo punto confronto tutti gli stati valori con quelli precedenti, se sono migliori allora faccio un altro giro, loppando fino a quando gli stati valori sono uguali al precedente, il che identifica la policy migliore.

Ma cosa vuol dire nella pratica?

Supponiamo di avare uno stato "s" e un'azione "a1" che porta in tre stati (s',s2, s3), dove per ognuno dei tre stati avviamo una probabilità di entrare in ciascuno stato con una relativa reward, abbiamo anche il valor medio totale dello stato Vπ di ciascun stato che era stato precedentemente calcolato applicando la policy. (vedi schema sotto riportato)

Ora per ogni azione (es. a1 e a2) voglio calcolare il valore medio dell'azione stessa che significa calcolare il valore delle "cose/fatti" che possono accadere pesati per le probabilità. Nell'esempio  sopra riportato significa prendere la probabilità che accada s' con la relativa reward r dato lo stato s con l'azione a1, ovvero:

p(s',r | s, a1)*(r+Vπ(s')) -> probabilità di andare in s' con l'azione a1 che moltiplica la somma della reward ottenuta per andare nello stato s' + il valore medio totale dello stato s'.

Questa operazione va ripetuta per ogni stato raggiunto dall'azione a1, ovvero nel nostro caso s',s2, s3 e sommata per questi tre stati quindi:

Qπ(s,a) = Σ (xx) p(sxx,r | s, axx)*(r+Vπ(sxx)) dove xx è s',s2,s3

Poi analogamente calcoliamo il Qπ(s,a2) e ne calcoliamo il massimo tra argmax (Qπ(s,a),Qπ(s,a2)) e scegliamo l'azione associata al Qπ massimo. In questo modo andiamo a miglioare la policy in maniera "greedy" ovvero cercando di massimizzare il valore. Il nome di questo algoritmo di chiama "policy iteration". Il cui pseudo codice è sotto riportato:

L'algoritmo alterna la valutazione (evaluation) della policy al improvement fino a che non ottengo la policy.

dove:

1) inzializza i valori randomicamente e seleziona una policy casuale

2) applica la valutazione delle policy, ovvero calcola V_pi

3) miglioramento, ovvero:

• facciamo un ciclo sugli stati S (detta anche "sweep") -> NB essendo pianificazione di un MDP a stati finiti rende la cosa fattibile, in reatà in giochi come "go" non è possibile in quanto gli stati sono un numero enorme, ma questa è un'altra storia)
• ciclo su tutte le azioni dello stato che sto valutando
  • salvo la vecchia azione (V(sxx)
  • effettuo la nuova azione e vedo quale valore V(sxx) otttengo
  • confronto vecchia e "nuova funzione valore" V(S) se il valore della nuova azione è miglioare allora l'agoritmo non ha  ancora trovato la policy migliore e quindi aggiorno la policy con l'azione miglioare e continuo a looppare
• fatti passare tutti gli stati se la policy non è stabile riparto dal punto 2
• in generale il tutto looppa finchè i valori non convergono il che significa che tra uno sweep e l'altro non ci sono grandi variazioni

Ricordo che la pianficazione si può applicare solo quando disponiamo del modello, che è il caso più facile e poco probabile che accada nel RL.

Di seguito l'algoritmo completo

from envs.gridworld import GridworldEnv
import  numpy as np


def policy_evaluation(policy, env, discount_factor=1.0, theta=0.001):
    """

    :param policy: [A,S] matrice di shape (rango = 29  a due domensioni che rappresenta la policy, dove sulle riche ci sono gli
                   stati e sulle colonne le azioni
    :param env: rappresentazione dell'ambiente
    :param discount_factor: fattore di sconto gamma
    :param theta: valore che termina la valutazione della policy una volta che la funzione stato valore è sotto questa soglia
    :return: ritarna la tabella stato valore (V) contenente i valori ottimali per arrivare allo più efficacemente allo stato terminale
             in pratica l'algoritmo incentiva ad andare verso lo stato il cui valore è più alto, es. tra due stati che valgono
             rispettivamente- 14 e -20 si va verso il valore pià grande ovvero -14.

    NOTA: - le azioni sono: 0 = su, 1 = dx, 2 = giù, 3 sx
          - la reward è sempre -1 tranne negli stati terminali
          - negli stati terminali le azioni non effettuano spostamento di stato.
    """

    # inizializzamo la funzione stato valore V, per semplificare la vita li portiamo a zero
    # dove il valore è il valore di OGNI STATO
    V = np.zeros(env.nS)

    # il ciclo deve fermarsi solo quanto la qta delta calcolata è minuore o uguale a theta
    passaggi = 0
    while True:
        delta = 0
        passaggi += 1


        # per ciscuno stato effettuo un "full backup"
        # questo primo ciclo fa passare tutti gli stati
        for stato in range(env.nS):
            v_appo = 0

            # questo il ciclo fa la sommatoria delle azioni
            # ovvero esegue tutte le azioni possibili nello stato s
            azioni_stato = enumerate(policy[stato])
            for azione , policy_prob in azioni_stato:

                # per ciascuna azione chiedo all'ambiente in quale stato finisco, la probabilità di finirci, la ricompensa
                # e se eventualmente è lo stato finale
                # NB: la situazione NON è vera in quanto stiamo facendo "esperienza" senza fare un passo, questo non è
                # vero RL è pianificazione
                # Da notare che questo ciclo è utile solo nel caso in cui a fronte di una azione ci possono essere diversi
                # stati destinazione con diverse probabilità, nel nostro caso ci sarà sempre e solo uno stato destinazione
                # con probabilità (env_prob) pari a 1
                for env_prob, next_state, reward, done in env.P[stato][azione]:

                    # equazione di Bellman
                    # probabilità dell'azione per la probabilità della transizione
                    v_appo = v_appo + policy_prob * env_prob * (reward + discount_factor * V[next_state])

            # delta misura l'errore su tutti gli stati, ovvero misura la differenza tra tutti gli
            # nella passata precedente N-1 e l'attuale N.
            # Nella pratica significa che per ogni stato il delta massimo trovato è quello indicato nella varibile
            # e quindi potrà poi essere comparato con theta per terminare la valutazione della policy
            delta = max(delta, np.abs(v_appo - V[stato]))
            V[stato] = v_appo

            # stampo la tabella degli stati
            # vr = V.reshape(env.shape).round(3)
            # print(vr,stato,passaggi,'%5.15f' % delta)
            # input()

        # finiamo la valutazione una volta che il valore è sotto la soglia theta
        if delta < theta:
            break

    return np.array(V), passaggi


def policy_improvment (env, policy,  policy_evaluetion_fn, discount_factor=1.0):
    """
    Funzione che migliora la policy iterativamente

    :param env: ambiente openAI
    :param random_policy: passiamo una policy iniziale
    :param policy_evaluetion_fn: funzione che valuta la policy e restituisce gli stati funzione valore V
    :param discount_factor: fattore di sconto gamma
    :return: ritorna una tupla che che tiene la nuova policy ottimale, gli stati valori e il totale passaggi effettuati
    """
    def one_step_lookahead(state, V):
        """
        funzione helper che calcola il valore di tutte le azioni dato uno stato

        :param state:
        :param V:
        :return: Q-value -> un vettore di lunghezza env.nA ovvero tutte le azioni possibili nello stato che contiene il valore funzione stato per ogni azione.
        """
        A = np.zeros(env.nA)
        # prendo tutte le azioni possibili nello stato passato in input alla funzione
        for a in range(env.nA):

            # come reagisce l'ambiente in quello stato
            # per ogni azione ottengo il valore totale medio
            # NB: interrogo l'ambiente e sarà lui a dirmi con quella azione in quali stati andrò e con quale probabilità e reward
            for prob, next_state, reward, done in env.P[state][a]:
                # calcolo il valore medio di tutti gli stati raggiungibili effettuando l'azione "a".
                A[a] += prob * (reward + discount_factor * V[next_state])
        return A

    passaggi = 0
    # ciclo di controllo.
    while True:

        passaggi += 1

        # valutiamo la policy
        V, psg = policy_evaluation_fn(policy, env, discount_factor)

        # setto il flag che mi interromperà il loop while
        policy_stable = True

        # estraggi tutti glistati
        # SWEEP
        for s in range(env.nS):

            # effetuo lo "one step ahead" per capire quali valori mi restituisce l'azione che ho deciso di
            action_values = one_step_lookahead(s, V)

            ############# calcolo l'azione migliore
            # IMPROVMENT
            #############
            best_a = np.argmax(action_values)

            # sceglo l'azione con probabilità maggiore tra quelle presente nella VECCHIA (attuale) policy
            # per quello stato, nella pratica estrae l'indice
            prev_policy_action = np.argmax(policy[s])

            # confronto l'azione delle vecchia policy con quella trovata dall'improvment e verifico se coincidoni
            # se non coincidono allora la policy non è ancora stabile e quindi non ottimale.
            if prev_policy_action != best_a:
                policy_stable = False

            # setto l'indice dell'azione che massimizza il valore calcolato a 1 per cambiare la policy ottimizzandola
            policy[s] = np.zeros(env.nA)
            policy[s][best_a] = 1

        # se la policy è stabile allora abbiamo trovato quella ottimale, quindi interrompo il ciclo principale ed esco
        if policy_stable:
            break


    return policy, V, passaggi


# 0 su 1 dx 2 giù 3 sx
# instanzio l'ambiente griglia
env = GridworldEnv([4,4])

print (env.nS)
print (env.nA)
env.reset()
env._render()
env.step(1)
print()
env._render()
env.step(1)

# definiamo una polcy generica, in pratica per ogni stato del mondo griglia associo 4 probabilità di eseguire una azione, le probabilità sono tutte al 25%
random_policy = np.ones( [env.nS, env.nA])/env.nA
print(random_policy)

policy_ottimale, V, passaggi = policy_improvment (env, random_policy, policy_evaluation)
#V,passaggi = policy_evaluation(random_policy, env)



v = V.reshape(env.shape).round(0)
print(v,passaggi)
#
print()
print(policy_ottimale)

(https://www.youtube.com/watch?v=QY3yxYyK4wM&list=PLMee1hSjLKdAL16E-7EzqHXsGOgzo8iro&index=13)

Iterazione di valore 

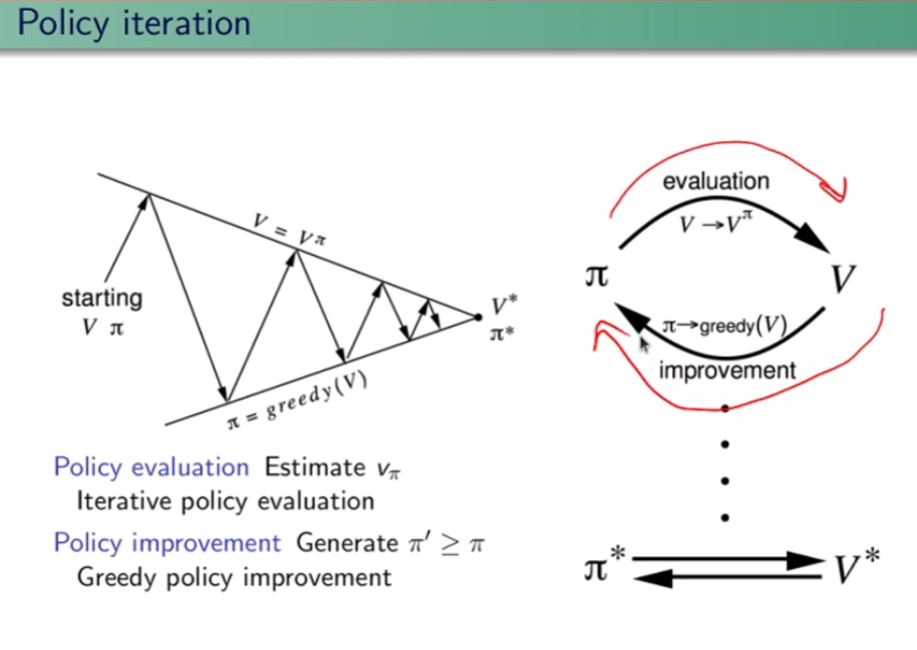
Con queste tipologie di algoritmi vogliamo ottimizzare le policy combianando la policy evaluation e la policy improvement.

Nel iterazione della policy ricordiamo che l'algoritmo è diviso in due parti, la prima che riguarda la valutazione della policy (evaluation) e la seconda che la migliora agendo in maniera "greedy" ovvero scegliendo l'azione che massimizza il valore medio atteso prendendo la argmax dei valori restituiti dal "one step look ahead".

Nella iterazione di valore invece l'alogoritmo di semplica e indirettamente si ottimizza combianando i due step secondo lo pseudo codice sotto riportato:

che in pratica applica l'equazione di Bellman sostituendo direttamente il valore medio atteso della funziona stato valore.:

 di seguito l'algorirmo rivisto, la differenza in termini di performace rispetto al precedente è notevole.

from envs.gridworld import GridworldEnv
import numpy as np

import time

# funzione per misurare il tempo di esecuzione di una funzione tramite un decorator
#  basterà1:
#  1) importare la funzione -> from objs.TimerDecorator import timing_decorator
#  2) decorare la funzione da misurare con @timing_decorator
def timing_decorator(func):
    def wrapper(*args, **kwargs):
        start = time.time()
        original_return_val = func(*args, **kwargs)
        end = time.time()
        print("time elapsed in ", func.__name__, ": ", end - start, sep='')
        return original_return_val

    return wrapper

from envs.gridworld import GridworldEnv
import numpy as np

from utils.TimerDecorator import timing_decorator


@timing_decorator
def value_itaration(env, theta = 0.00001, discount_factor=1.0):
    """
    Funzione che migliora la policy policy_improvment

    :param env: ambiente openAI
    :param theta: valore che termina la valutazione della policy una volta che la funzione stato valore è sotto questa soglia
    :param discount_factor: fattore di sconto gamma
    :return: ritorna una tupla che che tiene la nuova policy ottimale, gli stati valori e il totale passaggi effettuati
    """

    def one_step_lookahead(state, V):
        """
        funzione helper che calcola il q-value (valore) di tutte le azioni dato uno stato

        :param state:
        :param V:
        :return: Q-value -> un vettore di lunghezza env.nA ovvero tutte le azioni possibili nello stato che contiene il valore funzione stato per ogni azione.
        """
        A = np.zeros(env.nA)
        # prendo tutte le azioni possibili nello stato passato in input alla funzione
        for a in range(env.nA):

            # come reagisce l'ambiente in quello stato
            # per ogni azione ottengo il valore totale medio
            # NB: interrogo l'ambiente e sarà lui a dirmi con quella azione in quali stati andrò e con quale probabilità e reward
            for prob, next_state, reward, done in env.P[state][a]:
                # calcolo il valore medio di tutti gli stati raggiungibili effettuando l'azione "a".
                # equazione di "punto fisso"
                A[a] += prob * (reward + discount_factor * V[next_state])
        return A

    # inizializziamo gli stati con dei valori casuali a piacere (array di N stati)
    V = np.zeros(env.nS)
    while True:
        # inizializzo la variabile che condizione lo stop del loop
        delta = 0

        # aggiornare di stati
        for s in range(env.nS):
            # guardo uno step avanti restituendo la funzione stato valore di ogni azioni che può essere fettuata nello stato
            best_action_value = np.max(one_step_lookahead(s,V))

            # confronto l'azione con i valore dello stato nell'itezione precedente
            delta = max(delta, np.abs (best_action_value - V[s]))

            # salvo lo stato valore
            V[s] = best_action_value

        # se il delta è sotto theta allora i valori sono prossimi alla convergenza desiderata
        if delta < theta:
            break

        # ora dagli stati valore ricavo la policu V*(s) -> Q*(s,a)
        # inizilizzo la policy
        policy = np.zeros([env.nS,env.nA])
        for s in range (env.nS):
            azione = np.argmax(one_step_lookahead(s,V))
            policy[s][azione] = 1.0

        return policy, V


# 0 su 1 dx 2 giù 3 sx
# instanzio l'ambiente griglia
env = GridworldEnv([4, 4])

# print(env.nS)
# print(env.nA)
env.reset()
# env._render()
# env.step(1)
# print()

policy_ottimale, V, = value_itaration(env)
# V,passaggi = policy_evaluation(random_policy, env)

print(V)
#
# print()
print(policy_ottimale)

Esercizio 2

Abbiamo un certo capitale inferiore a 100 (es. 99 o 1 o 44) e lo scopo è arrivare esattamente a 100. (valori oltre il 100 non sono considerati, il goal è esattamente a 100) Possiamo scommetere solo il capitale a nostra disposizione lanciando una monetina scommettendo quello che vogliamo sulla base di quello che abbiamo. (es. ho 70 lancio la monetina e scommetto per es. 30 per arrivare a 100, se perdo vado a 40 se vinco vado a 100 e ho terminato il gioco vnicendo. Ovviamente se arrivo a zero ho perso.

Il problema può essere modellato come un MDP, senza 1) fattore di sconto, 2) episodico, ovvero da traiettorie (successione di azioni, rewards e stati) di lunghezza finita che si concludono in uno (o più) stato/i terminale/i raggiungible/i e 3) finito ovvero che stati e azioni sono finiti.

In generale quando le ricompense sono tutte zero, tranne che nella transizione dallo stato precedente allo stato terminale e lo stato terminale stesso, dove in questo caso vale 1, allora la funzione stato valore indica la probabilità di vittoria in quello stato.

Ricodiamo che: il valore dello stato è media con la probabilità di tutte le traiettorie possibili della ricompensa totale.

import numpy as np

"""
Abbiamo un certo capitale inferiore a 100 (es. 99 o 1 o 44) e lo scopo è arrivare esattamente a 100. 
(valori oltre il 100 non sono considerati, il goal è esattamente a 100) Possiamo scommettere solo 
il capitale a nostra disposizione lanciando una monetina scommettendo quello che vogliamo sulla 
base di quello che abbiamo. (es. ho 70 lancio la monetina e scommetto per es. 30 per arrivare 
a 100, se perdo vado a 40 se vinco vado a 100 e ho terminato il gioco vincendo. 
Ovviamente se arrivo a zero ho perso.

Il problema può essere modellato come un MDP, senza 1) fattore di sconto, 2) episodico, 
ovvero da traiettorie (successione di azioni, rewards e stati) di lunghezza finita che 
si concludono in uno (o più) stato/i terminale/i raggiungible/i e 3) finito ovvero che 
stati e azioni sono finiti.

In pratica lo stato rappresenta il capitale posseduto, e in base a quello la policy dovrebbe
cercare di assumere il comportamento ottimale.

In prima battuta va definito il modello. Il modello restituisce sempre ricompensa 0 tranne
quando arrivo nello stato terminale 100. Notare che la ricompensa non è quanto stiamo guadagnando in 
quanto l'obiettivo è arrivare a 100 e non accumulare più soldi possibili.

"""

def values_iteration_for_gamblers(probab_monetina = 0.5 , theta=0.0001, discount_factor=1.0):
    """

    :param probab_monetina: probabilità che esca testa
    :param theta: valore delta di convergenza
    :param discount_factor: fattore di sconto

    :return: policy e funzione stato valore
    """


    def one_step_look_ahead(in_capital, V, rewards, probab_monetina, discount_factor):
        """
        In base allo stato in cui mi trovo, ovvero il capitale a mia disposizione, effettuo una possibile
        giocata per tutte le possibili giocate a mia disposizione. Ovvero se ho un capitale di 40, farò
        una giocata partendo dalla somma 1 fino al massimo a mia dispisizione. (ovvero 40)

        La funziona ci dice nella pratica per ogni azione fatta con il capitale passato quanto vale quella azione.

        :param capitale: capitale del giocatore (rappresentato dallo stato)
        :param V: stati valore
        :param rewars: ricompense

        :return: ritorna l'elenco dei valori medi ottenibili effettuato tutte le azioni nello stato ovvero
                 del capitale passato in input
        """

        # inizializzo le azioni possibili in ogni stato
        A = np.zeros(101)

        # passato il capitale a disposizione, calcolo tutte le possibili giocate da quella minima (1) al massimo
        # che posso giocare con il capitale a disposizione passato in input.
        # il min(capital, (100-capital)) serve per calcolare il capitale giocabile considerando che
        # non posso andare oltre 100 anche se il capitale a mia disposizione lo consetirebbe
        capitale_giocabile = min(in_capital, (100 - in_capital))

        # effettuo tutte le giocate possibili
        for giocata_in_soldi in range(1,capitale_giocabile+1):
            # a questo punto per ogni giocata vedo il valore medeio di quello che può succedere effettuando
            # tutte le giocate possibili.
            A[giocata_in_soldi] =      probab_monetina  * (rewards[in_capital + giocata_in_soldi] + V[in_capital + giocata_in_soldi] * pow(discount_factor, giocata_in_soldi)) \
                                + (1 - probab_monetina) * (rewards[in_capital - giocata_in_soldi] + V[in_capital - giocata_in_soldi] * pow(discount_factor, giocata_in_soldi))

        # array che indica per ogni azione fatta con il capitale a mia disposizione, quanto vale ciascuna azione.
        return A

    ######################
    ######## INIZIO ######
    ######################

    # creo un array di 101 elementi che rappresenta le rewards dove:
    # - l'elemento zero è lo stato di perdita del gioco -> stato terminale
    # - l'elemento 101  è lo stato di vincita del gioco -> stato terminale
    # tutti gli stati avranno una rewards pari a zero tranne l'ultimo (100) che avrà reward = 1
    rewards = np.zeros(101)

    # ricordo che è zero based, quindi l'elemento 100 è il 101
    rewards[100] = 1

    # inzializzo la funzione stato valore con dei valori a "caso" facciamo zero per facilitare
    V = np.zeros(101)

    # creo la policy ottimale
    policy = np.zeros(101)

    # ciclo principale
    while True:

        # inizializzo la variabile che verrà utilizzata per interrompere i ciclo di valutazione della policy
        # fino alla sua convergenza.
        delta = 0

        # simulo tutti le possibili giocate con tutti i possibili capitali a mia disposizione
        # fa passare tutti gli stati
        for giocata in range (1,100):

            # verifico quanto valgono tutte le giocate con il capitale simulato
            # faccio tutte le azioni possibili
            A = one_step_look_ahead(giocata, V, rewards, probab_monetina, discount_factor)

            # determino il valore della giocata più alto
            best_action_value = np.max(A)

            # verifico se la giocata è migliore della precedente
            delta = max(delta, np.abs(best_action_value-V[giocata]))

            # salvo il valore migliore nella funzione stato valore
            V[giocata] = best_action_value

        # verifico se interrompere il loop perchè la funzione stato valore sta converendo
        if delta < theta:
            break

    # questo ciclo indica come giocare in ogni stato, dove lo stato rappresenta il capitale posseduto
    # serve solo per identificare l'azione megliore da intraprendere basandosi sulle stati valori ottimali precedentemente
    # calcolatir
    for giocata in range (1,100):
        A = one_step_look_ahead(giocata, V, rewards, probab_monetina, discount_factor)
        best_action_value = np.argmax(A)
        policy [giocata] = best_action_value

    return policy,V

policy, V = values_iteration_for_gamblers(discount_factor=1)

# tampo la funzione valore
for i in range(101):
    if i % 10 == 0:
        print()
    print (" %i-%s"%(i,V[i]), end='')

print ()

# stampo la policy
for i in range(101):
    if i % 10 == 0:
        print()
    #print (" %i-%s"%(i,policy[i]), end='')
    print(" %i-%s" % (i,policy[i]), end='')
# print (policy)
# print (np.reshape(policy,(10,10)))