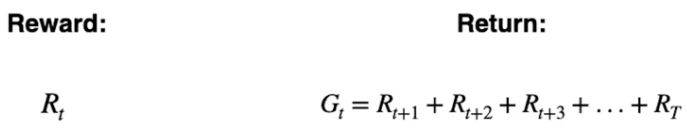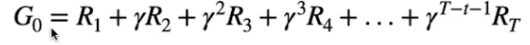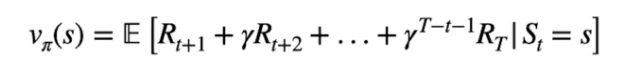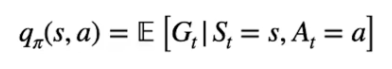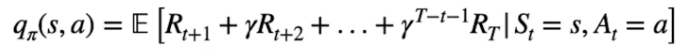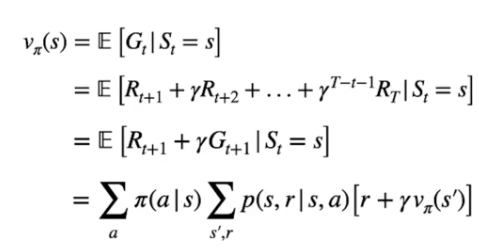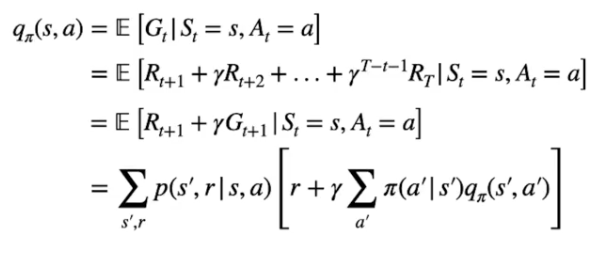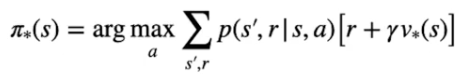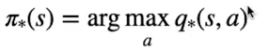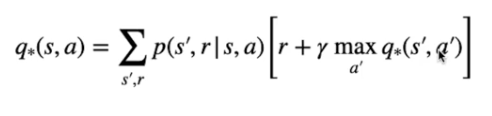Sessione 1 (Markov Decision Process)

Task di controllo

Il Task di Controllo è una sequenza di stati e azioni utili per addestrare l'algoritmo a risolvere un determinato problema.

Il task di controllo è compostato da:

1) Stati S(t) -  sono dei momenti nel tempo che assumono un certo valore

2) Azioni A -  sono le azioni eseguibili nell'ambiente basate sullo stato del task ed eseguite in un determinato momento nel tempo

3) Ricompensa R - è un valore che l'agente riceve dall'ambiente dopo aver eseguito un'azione

4) Agente - è l'entita che partecipa al task ne osserva lo stato ed effettua le azioni.

5) L'ambiente - è dove vengono eseguite le azioni da parte dell'agente a fronte delle quali vengono restituite ricompense e osservazioni.

Markov Decision Process

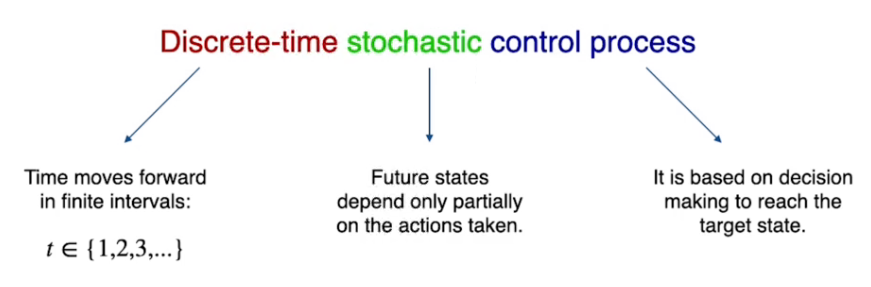
MDP sta per processo decisionale di Markov, è un template che serve per descrivere e gestire i task di controllo.

E' un controllo di processo stocastico basato su un tempo discreto.

L'MDP si basa su 4 elementi detti (S,A,R,P) ovvero:

• il set di possibili stati appartenenti al task
• il set di possibili azioni che possono essere intraprese in ciascun stato
  
• il set di possibili ricompense restituite a fronte di una azione intrapresa nello stato
• la probabilità di passare da uno stato all'altro eseguendo ogni possibile azione.

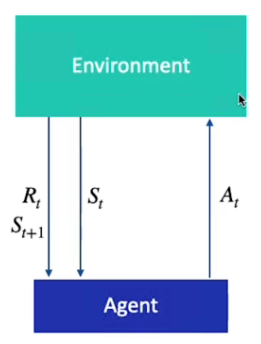
Di seguto viene data una rappresentazione grafica:

L'MDP ha una importante proprietà, ovvero la probabilità di visitare lo stato successivo dipende esclusivamente dallo stato attuale, il processo di Markov NON ha quindi memoria del passato.

MDP si diverifica nelle seguenti tipologie, ovvero:

• Finito
• Infinito
• Episodico
• Continuo

Nella versione versione finita le azioni, gli stati e le ricompense sono finite, mentre nella versione infinita uno o più dei valori citati sono infiniti. (un esempio di task finito è il labirinto griglia, mentre infinito può essere la guida automatica perchè il valore della velocità è infinito)

Nella versiona episofica l'episodio ha uno stato terminale mentre (come per es. l'uscita dal labirinto) nella versione continua non esiste uno stato stato terminale.

Traiettoria vs Episodio

La traiettoria è la seguenza: stato-azione-ricompensa,  partendo da uno stato iniziale fino a giungere ad un determinato stato che può anche essere quello finale. La traiettoria di identifica con la lettera greca tau 𝛕

L'episodio in invece è una particolare traiettoria che inizia da uno stato e finisce nello stato finale.

Ricompensa vs Ritorno

La ricompensa è il risultato immediato che l'azione produce.

Il ritorno è la somma delle ricompense che l'agente ottiente da un certo momento nel tempo (t) finchè lo stato è completato. Il ritorno è identificato dalla lettera G

Ovvero:

L'intento è quindi quello di massimizzare il ritorno atteso Gt

Fattore di sconto

Il fattore di sconto serve per massimizzare il ritorno nella maniera più veloce e ottimale possibile.

Per ottimizzare il ritorno bisogna quindi moltiplicare la rimpensa ottenuta da ciascuna azione per un fattore di sconto gamma (rappresentato dal carattere γ)  compreso tra zero e uno   γ ∈ [0,1]   elevato al momento nel tempo T, ovvero:

In questo modo vengono ridotti i valori di ricompensa ottenuti nel futuro, più è alto l'esponente più il valore nel futuro è ridotto, il tutto fino alla fine dell'episodio. (concetto derivato dalla matimatica finanziaria dove lo stesso valore nominare assume maggiore rilevanza quando è ravvicinato nel tempo, minore quando è distante rispetto a T0)

Se il valore di gamma valesse zero, allora non verrebbero considerate le ricompense future (perchè tutte portate a zero), e questa sarebbe una visione miope del task; al contrario del gamma valesse uno, allora non verrebbe calcolato l'episodio ottimale in quanto le ricompense non verrebbero scontate. Un valore gamma spesso utilizzato è 0.99 che garantisce - in genere - di massimizzare il ritorno, ovvero la somma delle ricompense scontate.

Policy

La policy è una funzione che prende in input uno stato e ritorna l'azione che deve deve essere eseguita nello stato stesso. E' rappresentata la lettera greca pigreco (π)

π : S -> A

Le due tipiche rappresentazioni in questo corso sono π(a|s) e π(s)

π(a|s) è la probabilità di eseguire un'azione "a" nello stato "s" -> ritorna una %

π(s) è invece l'azione "a" da eseguire nel dato stato "s" -> ritorna una azione "a"

Dipende dal contesto, in alcuni casi verrà restituita la probabilità in altri l'azione.

Tipologie di Policy

Le policy possono essere stocastiche o deterministiche.

Una policy deterministica sceglie sempre la stessa azione nello stesso stato, ovvero: π(s) -> a

es.  π(s) = a1

Una policy stocatica, sceglie un'azione sulla base di determinate probabilità, ovvero: π(s) = [p(a1),p(a1),........p(an)]

es. π(s) = [0.3,0.2,0.5] che significa che la policy ha la probabilità del 30% di scegliere la prima azione, del 20% la seconda e del 50% la terza.

La policy ottimale, rappresentata da π* il cui scopo è massimizzare la somma dei valori di ricompensa scontati alla lunga.

Stato valore

Il valore dello stato è il ritorno dello stato ottenuto interagendo con l'ambiente e seguendo la policy π fino alla fine dell'episodio, che si indica:

Vπ(s) = 𝔼[Gt | St=s]

di cui il dettaglio della formula:

dove è visibile l'esplosione del ritorno Gt come la somma delle ricompense scontate partendo dallo stato "s" per giungere allo stato finale "T".

Stato-azione (Q-Value)

Se invece vogliamo valutare una azione in un determinato stato, lo facciamo attraverso lo stato-azione Q.

Il valore Q nello stato "s" con l'azione "a" è il ritorno ottenuto eseguendo l'azione "a" partendo dallo stato "s" interagendo con l'ambiente tramite la policy π che seguiremo fino alla fine dell'episodio.

Di cui la formula generica

e la versione dettagliata:

L'equazione di Bellman

L'equazione di Bellman serve per trovare la policy ottimale per risolvere i task di controllo.

Bellman: Stato valore

Questa è l'equazione di Bellman che determina il valore di uno stato Vπ(s) associato alla policy, ovvero:

Le prime tre formule descrivono che il valore dello stato è il ritorno atteso Gt ottenuto seguendo la policy π partendo dallo stato "s".  (prima riga)

Possiamo espandere la definzione del ritorno Gt come la somma delle ricompense scontate da γ fino allo stato terminale. (seconda e terza riga)

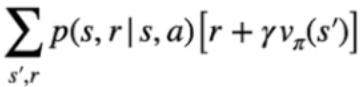Nell'espressione finale che ne deriva, troviamo la probabilità di eseguire ogni azione "a" condizionata nello stato "s"  seguendo la policy π ->  il tutto moltiplicato per   che rappresenta la probabilità di raggiungere ogni stato successivo (indicato con s' ) moltiplicato per la ricompensa ottenuta arrivando nello stato successivo sommata al valore dello stato successivo scontato dal fattore gamma.

Notare l'esistenza della ricorsione per quanto concerne il valore Vπ(s) -> Vπ(s') che può essere utilizzato durante la stesura dell'algoritmo.

Quindi vengono eseguite tutte le possibili azioni nello stato e calcolato il valore moltiplicando la probabilità nell'azione per il ritorno simmato al valore dello stato succissivo.

Bellman: Stato-Azione (Q-Value)

Questa è l'equazione di Bellman che determina il valore di uno stato-azione associato alla policy, ovvero:

Le prime tre formule descrivono che il Q-Value è il ritorno atteso Gt associato all'azione "a" ottenuto seguendo la policy π e partendo dallo stato "s".  (prima riga)

Possiamo espandere la definzione del ritorno Gt come la somma delle ricompense scontate da γ fino allo stato terminale condizionate allo stato "s" per l'azione "a". (seconda e terza riga)

Nell'espressione finale che ne deriva, viene indicata la probabilità di raggiungere ogni stato successivo s' sapendo che abbiamo scelto l'azione "a"  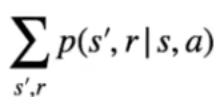->   il tutto moltiplicato per  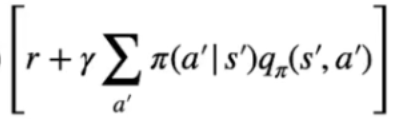 che rappresenta la ricompensa ottenuta raggiungendo lo stato successivo s' sommanta alla somma scontata di γ dei Q-values di ciascuna azione eseguita negli stati successivi pesata per la probabilità di eseguire l'azione in s' dettata dalla policy.

Anche qui viene espresso il Q-Value in termine di altri Q-Values in maniera ricorsiva.

Soluzione di un MDP

Per risolvere un MDP bisogna risolvere un task di controllo, il che significa massimizzare il ritorno atteso. Nella pratica bisogna massimizzare il valore di ogni stato V*(s) ->  o il valore di ogni Q-Value

Q*(s,a) -> 

Per massimizzare questi ritorni bisognerà quindi trovare la policy ottimale π* che è quella che sceglie le azioni ottimali in ogni stato e che porta il massimo ritorno atteso.

Di seguto viene rappresentata la formula che sceglie l'azione che restituisce il ritorno più alto

nel caso valore dello stato:

e nel caso stato-azione:

Ma pare che ci sia un problema, per trovare la policy ottimale servono dei valori ottimali, e vice versa, ovvero per trovare il valore dello stato ottimale o dello stato-azione ottimale (V* o Q*)  bisogna avere una policy ottimale... come fare?

Dobbiamo ottimizzare le equazioni di Bellman:

Per il valore degli stati V*:

ovvero:

Il valore ottimale dello stato è il ritorno atteso ottenuto seguendo la policy ottimale.

La policy ottimale in pratica sceglie l'azione che ritorna il valore più alto (di qui la max) associato al ritorno attesso.

Il ritorno atteso è la probabilità di accedere ad ogni stato successivo effettuando l'azione ottimale moltiplicato per la ricompensa ottenuta al raggiungemento dello stato s', sommato al valore di quello stato s' ottimale scontato da gamma.

o nel caso di dello stato-azione Q*

Nel caso invece del valore Q* ottimale per una azione "a" nello stato "s":

E' la somma pesata dei ritorni ottenuti raggiungendo ogni possibile stato successivo.

Il ritorno è la ricompensa ottenuta raggiungendo lo stato successivo sommato al valore ottimale massimo dello stato-azione successivo scontato da gamma.