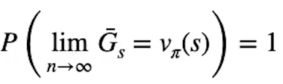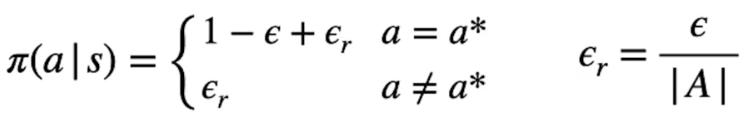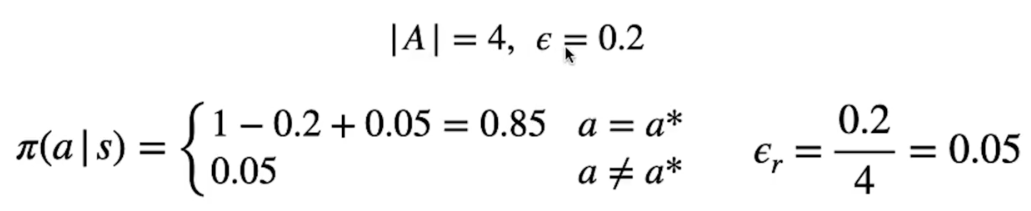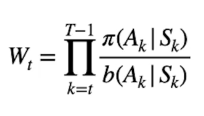Sessione 3 (Metodo Montecarlo)

Il Metodo Montecarlo (MC) migliora la policy iteragendo con l'ambiente e ottenendo dei ritorni (scontati da gamma) di cui viene calcolata la media. Per  la legge dei grandi numeri più osservazioni (e quindi ritorni) otteniamo più ci avviciniamo al valore ottimale atteso Vπ(S). 

Dalla formula si evince che il limite per n che tende a infinto dove n è il numero di misurazioni, genera una stima dei valori degli stati con probabilià 100% di essere ottimale.

Il MC ha dei vantaggi rispetto al DP (dynamic programmig spiegato nella sessione 2):

• la stima dei valori degli stati non dipende dagli altri
• il costo per stimare il valore di uno stato è indipendente dal numero toale degli stati

Nel caso del DP l'algoritmo bootstrappa il valore degli altri stati in modo da utilizzare una stima per produrne un'altra. Per questo la complessità di un algoritmo cresce esponenzialmente con il numero di stati.

Cosa molto importante MC non necessita del modello, la dinamica dell'ambiete sarà implicita nella nostra stima.

Per risolvere l'algorimo del MC verrà utilizzato il metodo, visto in precedenza anche con il DP detto "Generalized Policy Iteration".

Generalized Policy Iteration

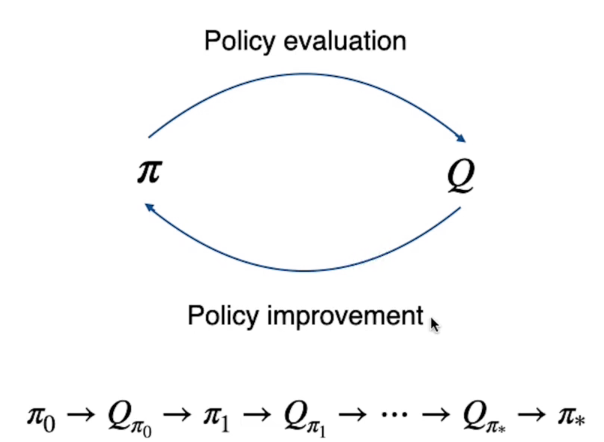
La GPI si basa sulla valutazione della policy (partendo da una che può essere randomica o arbitraria) per poi migliorarla e looppando fino a quando non si arriva a quella ottiamale.

MC si elabora generando un episodio la cui traiettoria parte dallo stato iniziale sino allo stato finale durante il quale vengono raccolte e sommate tutte le ricompense scontate gamma, per ogni stato dell'enviroment.

Bisogna quindi trovare la policy che sceglie l'azione con il Q-Value più alto, nella pratica dovremo tenere traccia nella tabella dei valori, non più i valori degli stati V(s) come nel DP, ma salveremo i valori delle azioni Q(s,a), ovvero dell'azione che massimizza il valore.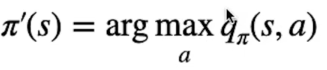

Il processo per MC diventerà quindi:

Dove la policy calcola i Q-Value  che viene a sua volta utilizzato per migliorare la policy in un ciclo continuo fino ai valori ottimali Q* e π*.

Exploration

Quindi la policy migliora sulla base dell'esperienza che agente effettua mentre interagisce con l'ambiente. L'esperienza che l'agente raccoglie dipende dalle azioni che effettua, e le azioni dipendono dalla policy utilizzata in quel momento. Per questo motivo avremo una policy π' che seleziona l'azione sulla base delle stime Q(s,a). E queste stime saranno sempre più accurate soprattutto mentre ci avviciniamo alle fasi finali dell'apprendimento. (a differenza delle fase iniziale dove invece sono inaccurate)

Immaginiamo il caso in cui l'azione è ottimale ma la sua stima Q(s,a) è pessima, allora la policy non la sceglierà in quanto la stima del valore è molto bassa. Si rende quindi necessario che tutte le azioni vengano scelte ogni tanto in maniera casuale per "esplorare" l'ambiente con scelte che normalmente non verrebbero effettuate, ma che possono migliorare la policy anche se apparentemente non nell'immediato. Tutto questo per scoprire eventuali azioni ottimali non considerate dalla policy in uso.

Quindi come mantenere l'esplorazione?

Beh, nella pratica abbiamo due opzioni:

1. La prima si chiama "exploring starts" e prevede che l'agente inizi la sua esplorazione in uno stato casuale dell'ambiente ed effettui un'azione iniziale casuale. Purtroppo non è una modalità molto realistica in quanto ci sono molti task che semplicamente non hanno questa possibilità. (soprattutto se parliamo del mondo reale)
2. La seconda si chiama "stocastic policies" ovvero vengono considerate le azioni che hanno una probabilità maggiore di zero, in questo modo ogni tanto vengono prese delle azioni "a caso" che potrebbero aiutare la policy a migliorare grazie al caso. (una sorta di evoluzione naturale della specie 😊 ) Queta seconda ipotesti è più realista e più facilmente implementabil.

Le policy stocastiche si suddivino in due tipologie:

• On-policy learning strategies: la quale genera l'esperienza basandosi nulla stessa policy che stiamo ottimizzando
• Off-policy learning strategies: la quale utilizza due policy distinte, una per esplorare l'ambiente e un'altra da ottimizzare

On-policy

Questo metodo segue una strategia che ogni tanto (randomicamente) effettua un'azione a caso, questa policy è chiamata epsilon-greedy. (ϵ-greedy)

In questa policy ogni azione ha la probabilità di essere eseguita maggiore di zero, ogni volta che bisogna scegliere un'azione ne scegliamo una casuale tra quelle disponibili nello stato con probabilità ϵ (che quindi deve essere abbastanza bassa) mentre nelle restanti probabilità 1-ϵ andiamo a scegliere l'azione con probabilità più alta, ovvero:

come si può vedere dalla formula la probabilità di scegliere l'azione ottimale  a* (quindi con la stima q-value più alta) è 1-ϵ sommato alla probabilità di scegliere un'azione casualmente, mentre, per contro, abbiamo la probabilità ϵ di sceglire una azione che potrebbe non essere ottiamale. ϵr rappresenta la probabilità di scegliare un'azione tra tutte le azioeni A disponibili.

Facciamo un esempio:

Abbiamo 4 possibili azioni e un ϵ del 20%, come sotto riportato:

La probabilità di sceglire l'azione con il valore Q(s,a) più alto è 80%.

Quando scegliamo un'azione a caso ϵr, la probabilità di scegliare cmq un'azione ottimale tra le 4 possibili è del 0,2/4 che sono le azioni possibili, ovvero del 5%. (o 0,05)

Per questo la probabilità di scegliere un'azione ottimale è del 0,85 (85%) perchè tra le 4 azioni c'è quella migliore (delle 4) che comunque va sommata a 1-ϵ.

Di seguito il pseudo codice che descrive l'alagoritmo:

In input viene passato epsilon e gamma (che ricordo rappresentare il fattore di sconto)

Vediamolo in codice Python.

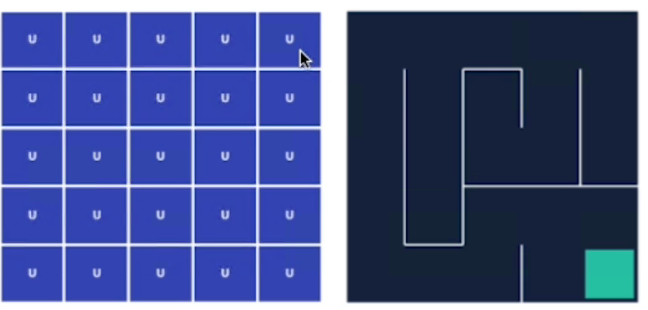
L'esempio di utilizzo è il classico labirinto 5x5, dove l'agente inizia nell'angolo in alto a sx e finisce il suo percorso in basso a dx.

Per prima inizializziamo la matrice che contiene le azioni effettuabili nello stato con valori zero il cui shape è 5x5x4 dove 5x5 sono gli stati mentre 4 sono le azioni effettuabili in ciascun stato. Il valore per inizializzare scelto è zero ma avrebbe potuto essere un qualsiasi valore arbitrario che il processo di apprendimento avrebbe comunque ottimizzato.

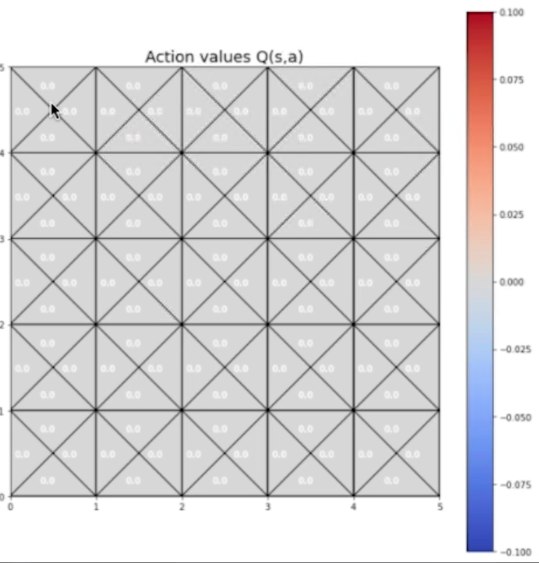
e ora plottiamo la rappresentazione dei Q-values associati a ciascuno stato:

Si possomo vedere i valori per 4 movimenti effettuabili in ciascono.

Creiamo una policy che scelga una azione dato uno stato e la probabilità di scegliere un'azione casuale. (ϵ)

La funzione che sceglie la policy,  effettua un'azione a caso tra le 4 disponibili se un numero compreso tra zero e uno, generato randomicamente, è inferiore al epsilon. (prima riga della funzione)

Nel caso invece nel quale si effettui l'azione migliore (1-ϵ) allora vengono in prima battuta estratti i 4 valori Q(s,a) associati allo stato passato in input. Di questi 4 valori viene scelto quello con il Q(s,a) più alto e, nel caso i valori più alti siano indentici tra loro, allora viene effettuata una scelta random tra questi. (vedi ultima riga della funzione)

NOTA: la funzione np.flatnonzero ritorna gli indici di un array che possiedono un valore diverso da zero.

giusto per cuiosità ho estrapolato la parte di codice che esegue l'azione con il Q-value più alto per far vedere come vengono gesiti i casi particolari come più valori identici massimi:

action_values = np.zeros((5,5,4))

def policy(state, epsilon=0.01):
    av= action_values[state]
    print (av.max())
    print (av == av.max())
    print ( np.flatnonzero(av == av.max()))
    return np.random.choice(np.flatnonzero(av == av.max()))


print (policy((0,0)))

0.0
[ True  True  True  True]
[0 1 2 3]
3

Visualizziamo la policy con i valori inizializzati, ovviamente essendo inizializzati l'azione di default è univoca per tutti gli stati.

ora definiamo l'algoritmo principale

def on_policy_mc_control(policy, action_values, episodes, gamma=0.99)
"""
Algoritmo di Montecarlo nella modalità on-policy
policy: funzione policy che scaglie le azioni, spiegata prima e che 
        attinge dalla tabella degli stati (action_values)
action_values: tabella contente tutte le azioni effettuabili per tutti gli stati dell'env
episodes: numero di episodi utili per far si che la policy migliori
gamma: fattore di sconto
"""

  # dizionario dove verranno salvati i valori associati alle coppie stato-azione
  sa_return={}

  # main loop
  for episode in range (1, episodes +1)

    # ricavo lo stato iniziale
    state = env.reset()
    
    # flag che determina la fine dell'episodio
    done = False
    
    # lista alla quale appendere i valori ritornanti dall'ambiente a fronte in una zione
    transtions = []

    # loop che gira finchè l'agente trova l'uscita e quindi termina il task
    while not done:
      
      # effettuo l'azione utilizzando la policy che abbiamo definito (cone random actions)
      action = policy(state, epsilon)

      # salvo le risposte dell'ambiente
      next_state, reward, done, _ = env.step(action)

      # salvo lo stao-azione e la reward ottenuta
      transtions.append ([state,action,reward])

      # salvo il prossimo stato da eseguire
      state = next_state
      
    # inizializzo il rtorno
    G = 0
    
    # calcolo il ritorno in modalità "backword" ovvero dall'ultimo al primo
    for state_t, action_t, reward_t in reverse(transtions)
      G = reward_t + gamma*G

      # se l'elemento non esiste nel dictionary allora lo creo con per la coppia stato-azione
      if not (state_t, action_t) in sa_retutns:        
        sa_returns[(state_t, action_r)] = []

      # aggiungo il ritorno 
      sa_returns[(state_t, action_r)].append(G)

      # salvo nella stato/azione la media dei ritorni per lo stato-azione
      action_vales[state][action] = np.mean (sa_returns[(state_t, action_t)])
      
        
    
# test
on_policy_mc_control(policy, action_values, episodes = 10000)
    
      

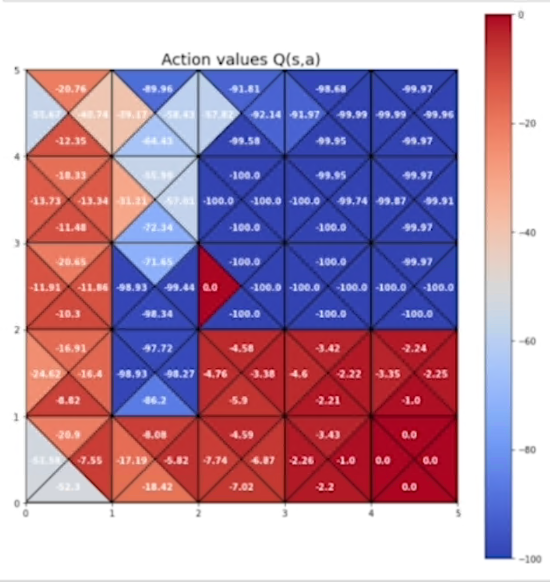
di seguito la tabella delle azioni ottimali negli stati:

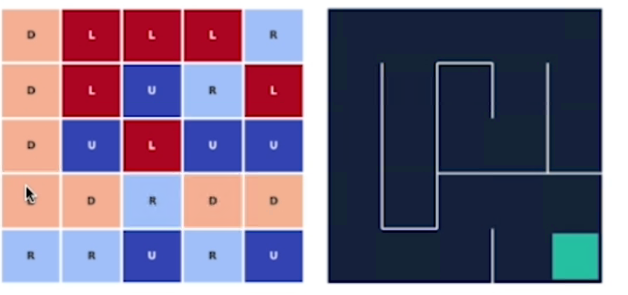
di seguito la mappa delle azioni migliori che portano alla fine del tastk

Oltre al  set delle azioni migliori si vede come negli stati non ottimali (in alto a dx)  l'agente le evita tranne per il fatto che ogni le esplora casualmente.

Ottimizzazione On-Policy

L'ottimizzazione consiste nel modificare l'algoritmo per aggiornare i valori degli stati in maniera più efficiente semplificando l'algoritmo, mantenendo allo stesso tempo la sua effeficacia.

Le differenze si sostanziano in:

1. La prima differenza consiste nel fatto che non teniamo traccia dei ritorni osservati dall'agente
2. La seconda invece nel "pushare lentamente" il valore della stima di una percentuale alpha (α) che moltipica la differenza tra il ritorno appena calcolato e il precedente valore stato-azione, ovvero: Q(s,a) = Q(s,a) + α[G - Q(s,a)]

Vediamo il pseudo-codice

l'implementazione

def on_policy_mc_control(policy, action_values, episodes, gamma=0.99, alpha=0.2)
"""
Algoritmo di Montecarlo nella modalità on-policy
policy: funzione policy che sceglie le azioni, spiegata prima e che 
        attinge dalla tabella degli stati (action_values)
action_values: tabella contente tutte le azioni effettuabili per tutti gli  stati dell'env
episodes: numero di episodi utili per far si che la policy migliori
gamma: fattore di sconto
alpha= parametro che muove lo stato valore di una percentuale che va in direzione del ritorno appena osservato
"""

  # main loop
  for episode in range (1, episodes +1)

    # ricavo lo stato iniziale
    state = env.reset()
    
    # flag che determina la fine dell'episodio
    done = False
    
    # lista alla quale appendere i valori ritornanti dall'ambiente a fronte in una zione
    transtions = []

    # loop che gira finchè l'agente trova l'uscita e quindi termoina il task
    while not done:
      
      # effettuo l'azione utilizzando la policy che abbiamo definito (cone random actions)
      action = policy(state, epsilon)

      # salvo le risposte dell'ambiente
      next_state, reward, done, _ = env.step(action)

      # salvo lo stao-azione e la reward ottenuta
      transtions.append ([state,action,reward])

      # salvo il prossimo stato da eseguire
      state = next_state
      
    # inizializzo il rtorno
    G = 0
    
    # calcolo il ritorno in modalità "backword" ovvero dall'ultimo al primo
    for state_t, action_t, reward_t in reverse(transtions)
      G = reward_t + gamma*G

      # ottengo il q-value dalla tabella dei valori
      qsa =  action_vales[state][action]

      # ottimizzazione, mi muovo nella direzione del valor appena calcolato
      action_vales[state][action] += alpha * ( G - qsa)
      
        
    
# test
on_policy_mc_control(policy, action_values, episodes = 10000)

Visualizzare la nuova tabella stati valore

Off-Policy

E' la seconda strategia (la prima è l'on-policy)  utile per mantenere il miglioramento e l'esplorazione. La logica è sempre quella di effettuare, ogni tanto, un'azione "sub-ottimale" e per questo motivo vengono utilizzate due policy separate.

Nell'apprendimento MC-Off Policy, andiamo quindi a separare la "Exploratory policy" b(a|s) dalla "Target policy" π(s,a) (quella da ottimizzare) 

La policy di esplorazione effettuerà quindi una traiettoria explorativa la cui esperienza verrà utilizzata dalla target per essere migliorata. π(s,a) <- arg max Q(s,a)

Nella pratica i valori della target policy verranno aggiornati sui campioni raccolti dalla exploration policy. Per funzionare, la exploratory policy deve raccogliere tutte le azioni che la target policy può effettuare. Quindi se la target ha una probabilità di effettuare un'azione > 0 allora anche l'exploratory deve avere questa probabilità. 

Ovvero: if π(s,a) > 0 allora b(s,a) >0 altrimenti ci potrebbero essere azioni che la target sceglie mentre la exploratory no, il che non farebbe migliorare la target.

Nella pratica viene calcolato il ritorno medio utilizzano la policy di eplorazione andando ad approssimare il valore Q(s,a) non della target policy. Per migliorare la target policy bisogna quindi utilizzare una tecnica chiamata "importance sampling" la quale va a stimare i valori attesi di una distribuzione (la target), lavorando con i campioni di un'altra (l'exploratory).

Importance sampling

Il metodo utilzzato per legare statisticamente le due policy è chiamato "Importance sampling" aka IS, consta nel moltiplicare il ritorno al tempo "t" per un valore chiamato "Wt" il cui valore è dato dal rapporto tra: tutte le probabilità generate allo stato k dalla target policy nell'effettuare le azioni, divisa dalla proprietà generata dalla exploration policy anch'essa nel scegliere le azioni.

E[ Wt x Gt | St = s] = Vπ(s)

In questo modo moltiplicando l'IS per il ritorno Gt andiamo ad approssimare il valore ottimale della target policy Vπ(s)

La regola di aggiornamento dei valori ottimali Q-values (s,a) è quella di tenere traccia della lista di tutti i ritorni osservabili,  poi quando c'è da aggiornare i valori Q si fa la media di tutti i ritorni G precedenti. Il ricalcolo però è inefficiente perchè necessita di un grosso quantitativo di memoria per salvare tutti i ritoni G.

Utilizzeremo quindi il metodo già visto nel MC On-Policy ottimizzato, che va a "spostare" lentamente lo stato valore verso il nuovo valore osservato:

solo che questa volta non utilizzeremo un valore alpha discrezionale invece verrà utilizzato l"Importance sampling" precedente descritto, normalizzato con la sommatoria C(s,a) di tutti i valori "importance samples" precedenti.

Per evitare distorsioni dovute ai valori di IS, lo si va a normalizzare divedendolo per tutti gli IS osservati per lo stato azione elaborati. (vedi immagine sopra) Questo manterrà gli aggiornamenti tra zero e uno.

Di seguito il pseudo codice:

E' simile all'online MC ma utilizza due policy e tiene un totalizzatore di "important sampling ratio C(s,a)" per tutti gli stati-azioni.

Passiamo ora all'implementazione

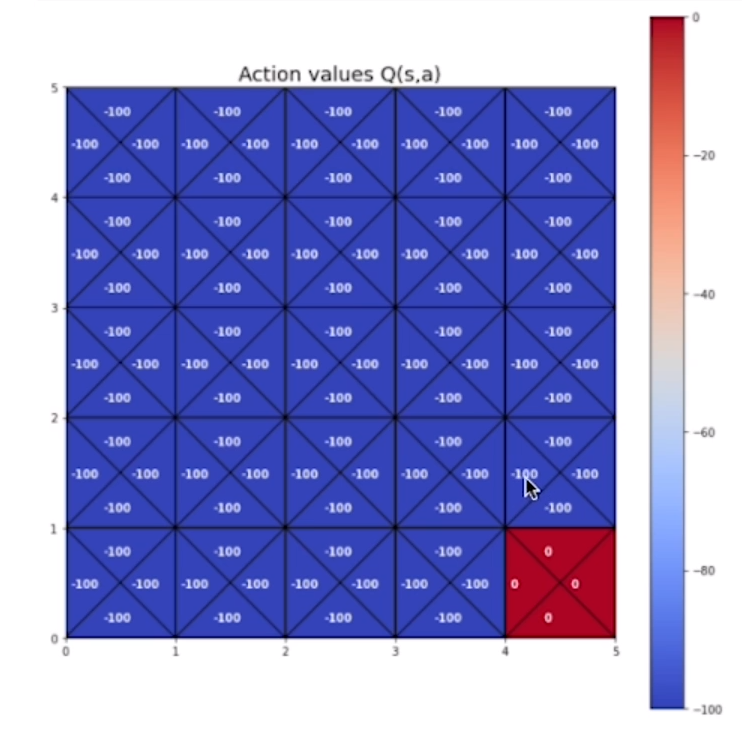
# inizializzazione della tabella Q-value (s,a) con valori arbitrari
action_values = np.full((5,5,4),-100)

# setto il valore del goal a zero
action_values [4,4,:] = 0.

e visualizziamo la tabella con i valori:

# creiamo la policy
# scegliere un valore a caso tra quelli pià alti
def target_policy(state):    
    av = action_values[state]
    return np.random.choice(np.flatnonzero(av == av.max()))

# creiamo una policy esplorativa
def exploratory_policy (state, espsilon=0.2):
  """
  state: id del valore azione
  espsilon: probabilità di intraprendere un'azione casuale
  """
    # definiaimo che ogni tanto casualmetne effettua un'azione casuale
    if np.random.random() < espsilon:
        return np.random.choice(4)
    else:
        # in caso in cui sceglie l'azione migliore
        return target_policy(state)


# implementiamo l'algoritmo MC-off policy
def off_policy_mc_control(action_values, target_policy, exploratory_policy, episodes, gamma=.99, espsilon=.2):
  """
  action_values: tabella stati azioni Q(s,a)
  target_policy: policy da ottimizzare
  exploratory_policy: policy che esplora casuale ogni tanto (espilon)
  episodes: numero di episodi
  gamma: fattore di sconto
  espsilon: probabilità di scelta di un'azione casuale
  """
  
    # creiamo una matrice dove verranno salvate le somme dei rapporti associati agli IS inizializzandola a zeroes
    # la matrice contiene un valore per ogni combinazioni di stato-azione 5x5 stati x4 valori a stato  
    csa = np.zeroes ((5,5,4))

    # ciclo per tutti gli episodi passati in input
    for episode in rage (1, episodes +1):
      
      # inizializzo il ritorno a zero
      G = 0

      # inizializzo l'importance sampling (rapporto tra le due policy)
      W=1

      # inizializzo le variabili del task
      state = env.reset()
      done = False      
      transition = [] # array dove vengono salvate le ossercazioni ritornate dell'env
    
      # loop che si ripete fino alla fine dell'episodio
      while not done:
        
        # usimo la exploratory policy
        action = exploratory_policy(state, espsilon)

        # eseguiamo l'azione "esplorativa"
        next_state, reward, done, _ = env.step(action)
        
        # salvo l'osservazione ritornata dall'env
        transition.append([state,action,reward])        

        # salvo lo stato per il prossimo giro
        state = next_state

      # utilizziamo l'esperienza ottenuta dall'esplorazione per migliorare la policy target
      # parto dalla fine del task e calcolo il ritorno G scontato da gamma 
      # L'ordine è inverso per facilitare il calcolo dei ritorno
      # Nella pratica faccio passare tutti gli stati-azioni che sono stati ritornati durante
      # la fase di esplorazione. Per ciascuno di essi calcolo:
      # 1) il rapporto IS
      # 2) uso il rapporto IS per "spostare" proporzionalmente il valore Q(s,a) verso il ritorno appena calcolato
      #    e lo sommo alla tabella stato-azione
      for state_t, action_t, reward_t in reversed(transition):
      
        # calcolo il ritorno scontato da gamma
        G = reward_t + gamma * G

        # calcolo l'important sampling W
        csa [state_t,action_t] += W

        # salvo il vecchio valore associato allo stato-azione
        qsa = action_values[state_t][action_t]

        # aggiorniamo i q-values spostando il valore
        action_values[state_t][action_t] += (W/csa[state_t][action_t]) * (G -qsa)

        # dopo il ricalcolo degli stati azioni riprovo la target policy e verifico  se l'azione è diversa da quella precedente
        # se così allora interrompo il miglioramento e riprendo con l'esplorazione con un altro episodio
        if action_t != target_policy(state_t):
          break

    
        # ricalcolo l'IS  
        W = W * 1 / (1-epsilon + epsilon/4 )