Tensore

Cosa è un tensore?

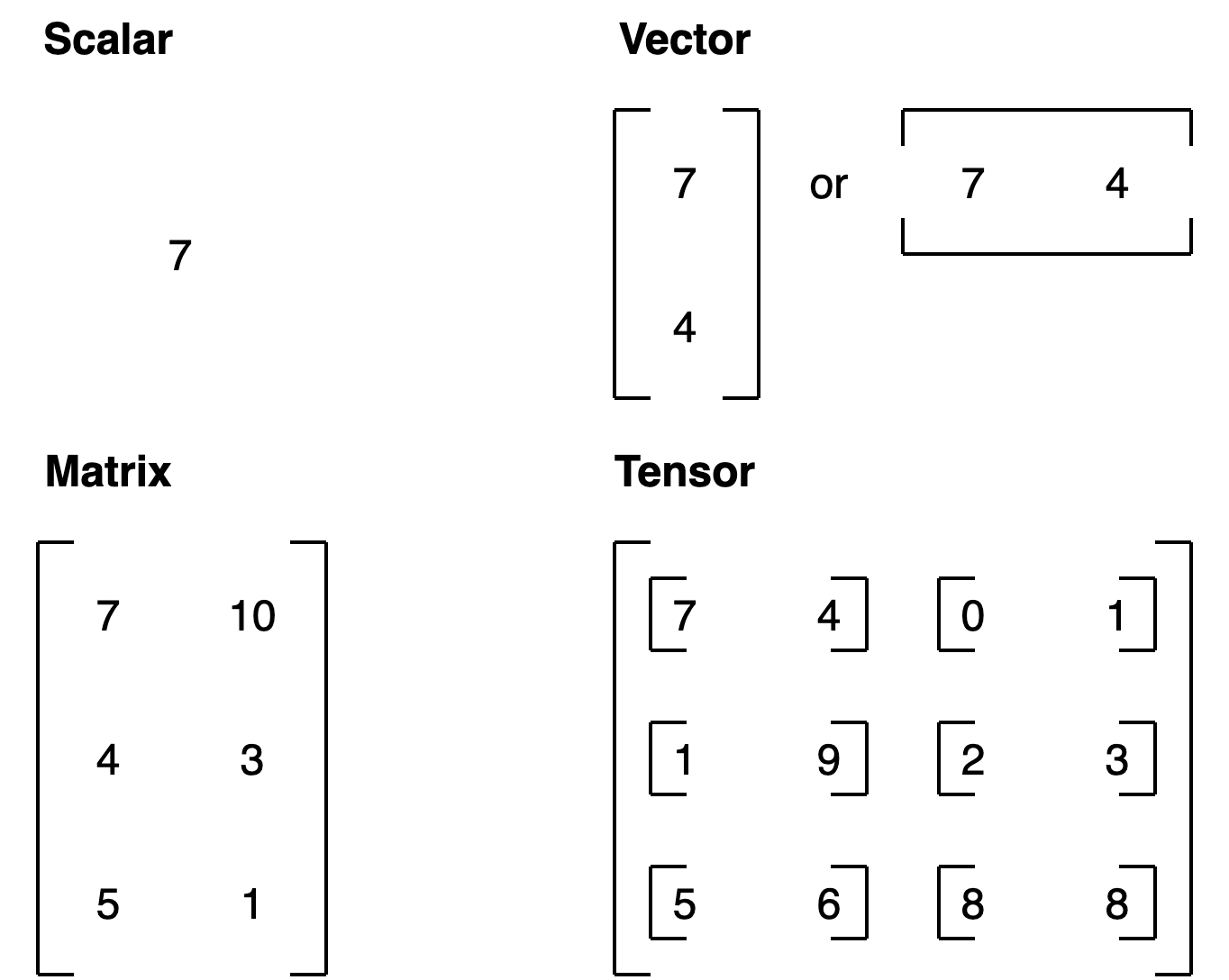
Il tensore è uno scalare (valore singolo), un vettore o una matrice multidimensionale, nella quale vengono storati i valori utilizzati da pytorch.

Nella pratica un tensore è la rappresntazione numerica in forma di array/matrici di un qualsiasi fenomeno esterno, sia esso per es. un'immagine, un suono o un range di valori numerici.

es:

# Scalar
cuda0 = torch.device('cuda:0')
scalar = torch.tensor(7, device=cuda0)
scalar

In questo caso istanzio uno scalare contenete il valore 7, da notere che, avendo un GPU vado a storare questo valore nella ram del GPU e non della cpu.

Di seguito un esempio di matrice

MATRIX = torch.tensor([[7, 8], 
                       [9, 10]], device=cuda0)
MATRIX

Le dimensioni del tensore

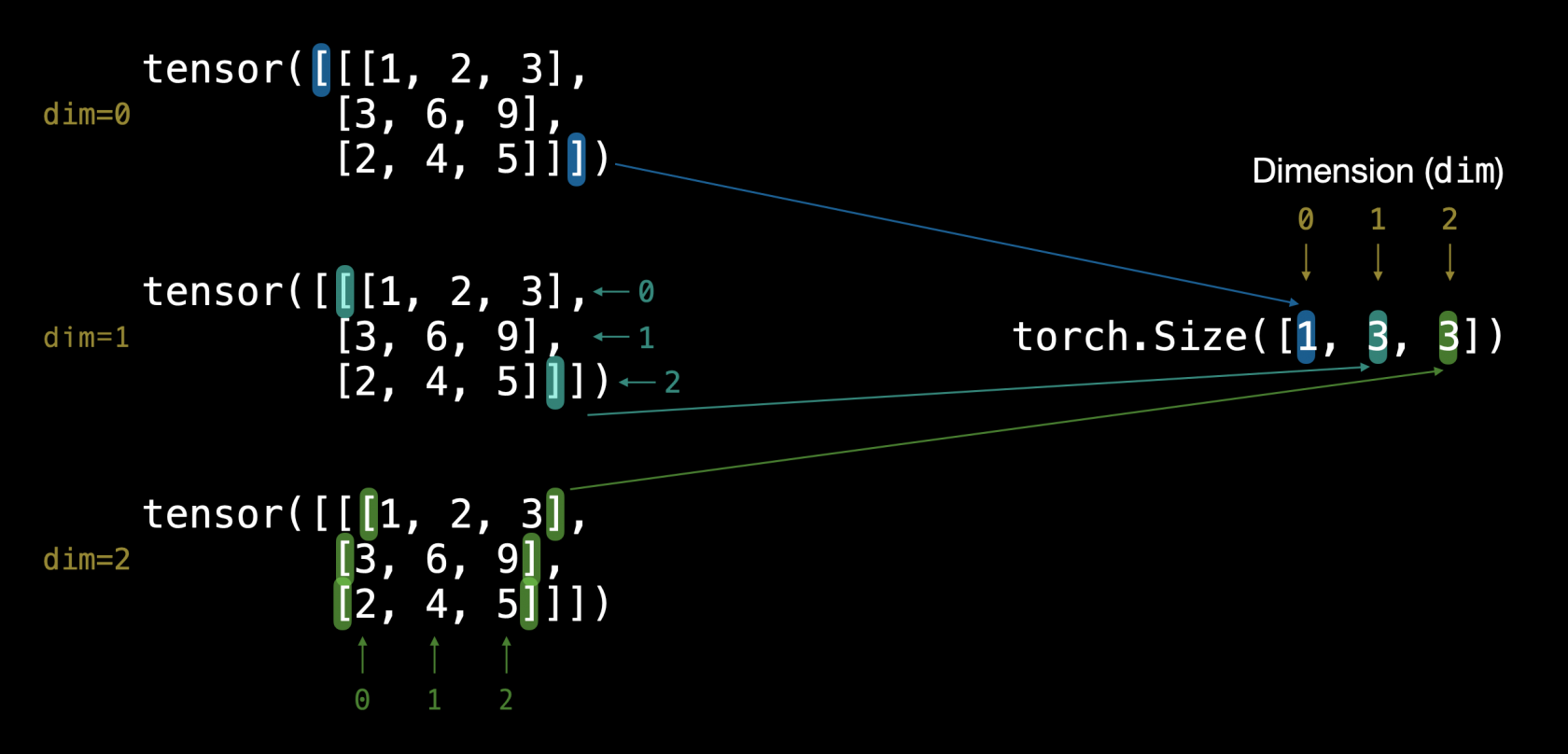
NB: cerchiamo di capire bene la differenza tra la dimention e la size. La dimension indica quanti livelli "innestati" sono definiti all'interno della matrice, mentre la size indica il numero totali di righe-colonne presenti nella matrice.

Tensori randomici

Sono molto utili nelle fasi iniziali del training , di seguito un esempio per la creazione:

random_tensor = torch.rand(3,4)


tensor([[0.1207, 0.8136, 0.9750, 0.5804],
        [0.4229, 0.6942, 0.4774, 0.5260],
        [0.2809, 0.1866, 0.8354, 0.7496]])

# oppure altro esempio:
  
import torch

cuda0 = torch.device('cuda:0')
random_tensor = torch.rand(2,3,4, device=cuda0)
print (random_tensor)

tensor([[[0.2652, 0.6430, 0.7058, 0.3049],
         [0.3983, 0.4169, 0.6228, 0.6622],
         [0.6239, 0.7246, 0.1134, 0.9273]],
        
        [[0.5454, 0.9085, 0.2009, 0.7056],
         [0.5211, 0.6397, 0.9299, 0.1871],
         [0.8542, 0.1733, 0.4378, 0.3836]]], device='cuda:0')

# dove si evince il tensore è di 2 righe ciascuna delle quali è composta
# a sua volta da  una matri di 3 righe per 4 colonne

se invce si vuole crare un tensore di zeroes.

zeros = torch.zeros(size=(3, 4))

Range di tesori

 Use torch.arange(), torch.range() is deprecated 
zero_to_ten_deprecated = torch.range(0, 10) # Note: this may return an error in the future

# Create a range of values 0 to 10
zero_to_ten = torch.arange(start=0, end=10, step=1)
print(zero_to_ten)
> tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

se vuole creare un tensore che la le stesse dimensioni di un altro

ten_zeros = torch.zeros_like(input=zero_to_ten) # will have same shape
print(ten_zeros)

DTypes

è il datatype che definisce i dati contenuto nel tensore

per vedere i tipi di datatypes: https://pytorch.org/docs/stable/tensors.html#data-types

# Default datatype for tensors is float32
float_32_tensor = torch.tensor([3.0, 6.0, 9.0],
                               dtype=None, # defaults to None, which is torch.float32 or whatever datatype is passed
                               device=None, # defaults to None, which uses the default tensor type
                               requires_grad=False) # if True, operations perfromed on the tensor are recorded 

float_32_tensor.shape, float_32_tensor.dtype, float_32_tensor.device

# Create a tensor
some_tensor = torch.rand(3, 4)

# Find out details about it
print(some_tensor)
print(f"Shape of tensor: {some_tensor.shape}")
print(f"Datatype of tensor: {some_tensor.dtype}")
print(f"Device tensor is stored on: {some_tensor.device}") # will default to CPU

tensor([[0.2423, 0.6624, 0.3201, 0.3021],
        [0.7961, 0.9539, 0.0791, 0.8537],
        [0.3491, 0.6429, 0.8308, 0.4690]])
Shape of tensor: torch.Size([3, 4])
Datatype of tensor: torch.float32
Device tensor is stored on: cpu

Forzare i tipi

Ovviamente è possibile cambiare il dtype per quei casi in cui le operazioni generano degli errori per es.

x = torch.arange(0,100,10)
print (x, x.dtype)
> tensor([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90]) torch.int64

ma la funzione media non accetta un tipo "long" per cui dovremmo formare il vettore a float come sotto riportato:

y= torch.mean(x.type(torch.float32))

print(y)

oppure

print( x.type(torch.float32).mean() )

>tensor(45.)

Operazioni con i tensori

NB: nelle operazioni con i tensori, es. le moltiplicazioni, posso effettuarle tra tipi diversi. (es. int16 x float32)

Le operazioni basi sono le classiche: +,-,*,/ e moltiplicazione tra matrici:

# Create a tensor of values and add a number to it
tensor = torch.tensor([1, 2, 3])
tensor + 10
tensor([11, 12, 13])

# Multiply it by 10
tensor * 10
tensor([10, 20, 30])
#Notice how the tensor values above didn't end up being tensor([110, 120, 130]), this is because the values inside the tensor don't 
#change unless they're reassigned.

# Tensors don't change unless reassigned
tensor
tensor([1, 2, 3])
#Let's subtract a number and this time we'll reassign the tensor variable.

# Subtract and reassign
tensor = tensor - 10
tensor
tensor([-9, -8, -7])

# Add and reassign
tensor = tensor + 10
tensor
tensor([1, 2, 3])
PyTorch also has a bunch of built-in functions like torch.mul() (short for multiplcation) and torch.add() to perform basic operations.

# Can also use torch functions
torch.multiply(tensor, 10)
tensor([10, 20, 30])
# Original tensor is still unchanged 
tensor
tensor([1, 2, 3])
#However, it's more common to use the operator symbols like * instead of torch.mul()
# Element-wise multiplication (each element multiplies its equivalent, index 0->0, 1->1, 2->2)
print(tensor, "*", tensor)
print("Equals:", tensor * tensor)

tensor([1, 2, 3]) * tensor([1, 2, 3])
Equals: tensor([1, 4, 9])

Moltiplicazione tra matrici

One of the most common operations in machine learning and deep learning algorithms (like neural networks) is matrix multiplication.

PyTorch implements matrix multiplication functionality in the torch.matmul() method.

Regole della moltiplicaazione di matrici

Regola della dimensione interna

La dimensione interna DEVE essere la stessa, ovvero, se abbiamo una matrice (3,2) e un'altra matrice di (3,2)

la moltiplicazione genererà un errore in quanto le dimensioni interne non coincidono.

Per dimensione interna si intende (3,2) x (2,3) in questo caso il 2, dove nella prima matricie sono le colonne mentre nella secondo le righe. (nel primo esempio erano invece diverse e quindi non è possibile effettuare la moltiplicazione.

Regola della matrice risultante

La shape della matrice risultante è pari alle dimensini esterne delle due matrici.

Ovvero nel caso di matrici (2,3) x (3,2) che quindi soffisfano la regola della dimensione interna, la risultante sarà una matrice la cui dimensione sarà la dimensione esterna, quindi (2,2)

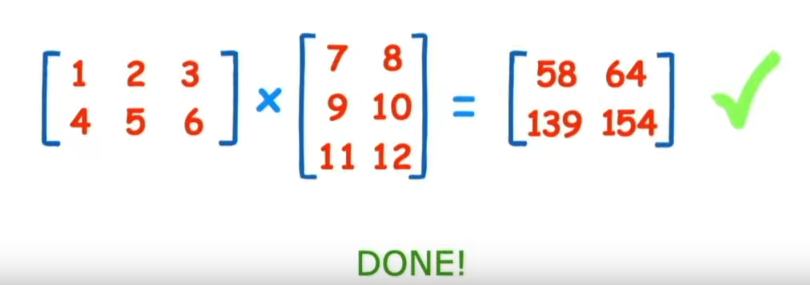
Come moltiplicare due matrici

Di seguito viene mostrato graficamente come moltiplicare due matrici:

....

Differenza tra "Element-wise multiplication" e "Matrix multiplication".

Element wise moltiplication moltiplica ogni elemento mentre invece matrix multiplication effettua il totale delle moltiplicatione delle matrici.

tensor variable with values [1, 2, 3]:

Operation	Calculation	Code
Element-wise multiplication	`[11, 22, 3*3]` = `[1, 4, 9]`	`tensor * tensor`
Matrix multiplication	`[11 + 22 + 3*3]` = `[14]`	`tensor.matmul(tensor)`

# Element-wise matrix multiplication
tensor * tensor
>tensor([1, 4, 9])

# Matrix multiplication
torch.matmul(tensor, tensor)
> tensor(14)

# Can also use the "@" symbol for matrix multiplication, though not recommended
tensor @ tensor
>tensor(14)

Manipolazione dello shape

Coonsideriamo il caso


tensor_A = torch.tensor([[1, 2],
                         [3, 4],
                         [5, 6]], dtype=torch.float32)

tensor_B = torch.tensor([[7, 10],
                         [8, 11], 
                         [9, 12],
                         [13,14]], dtype=torch.float32)

se eftettuiamo la motiplicazione dei due, per le due regole sopra citate, verrà generato un errore in quanto la dimensione interna non matcha:

errore -> torch.matmul(tensor_A, tensor_B) in quanto abbiamo una moltiplicare di (3,2) x (4,2) che non coincidono internamente.

ma allora che fare? ebbene in questo caso possiamo far coincidere le dimensioni interne di uno dei due tensori utilizzando la funzione "transpose", come di seguito

torch.matmul(tensor_A, tensor_B.T) dove il metodo .T effettua la traspose del tensore B rendendolo compatibile con A, ovvero:

tensor([[ 7.,  8.,  9., 13.],
        [10., 11., 12., 14.]])

che traspone la (4,2) in (2,4) e quindi l'output della moltiplicare sarà:

# effetto la moltiplicazione ora con la transposizione è diventato -> torch.Size([3, 2]) * torch.Size([2, 4])
torch.mm(tensor_A*tensor_A.T)

Output:

tensor([[ 27.,  30.,  33.,  41.],
        [ 61.,  68.,  75.,  95.],
        [ 95., 106., 117., 149.]])

Output shape: torch.Size([3, 4])

che soddispafa la prima regola (dimensione interna) e la seconda regola (dimensione tensore risultate pari alla dimensione esterna)

NOTA: per fare delle prove andare sul sito http://matrixmultiplication.xyz/

Aggregazione del tensore

Oltre alla moltiplicazione abbiamo altri tipi di operazioni comuni che possono essere effettuate sui tensori ovvero:

min, max, mean, sum, ed altro... che nella pratica si tratta di invocare il metodo dell'oggetto "torch" es. torch.mean(tensore)

NOTA: Può essere che questi metodi diano degli errori sui tipi, es il metodo mean non accetta un dtype long, per questo motivo il tipo può essere convertito "al volo" tramite il metodo type, es. torch.mean ( X.type(torch.float32) ) -> che lo casta a floating 32.

Posizionamento del min e del max

Se vogliamo sapere l'indice del valore minimo o massimo all'iterno del tensore allora toch ci mette a disposizione il metodo argmin es.

#Create a tensor
tensor = torch.arange(10, 100, 10)
print(f"Tensor: {tensor}")

# Returns index of max and min values
print(f"Index where max value occurs: {tensor.argmax()}")
print(f"Index where min value occurs: {tensor.argmin()}")

Tensor: tensor([10, 20, 30, 40, 50, 60, 70, 80, 90])
Index where max value occurs: 8
Index where min value occurs: 0

Reshaping, stacking, squeezing e un squeezing

Lo scopo di questi metodi è manipolare il tensore in modo da modificarne lo "shape" o la dimensione. Di seguito viene riportata una breve descrizione dei metodi.

Metodo	Descrizione (online)
torch.reshape(input, shape)	Reshapes `input` to `shape` (if compatible), can also use `torch.Tensor.reshape()`.
torch.Tensor.view(shape)	Returns a view of the original tensor in a different `shape` but shares the same data as the original tensor.
torch.stack(tensors, dim=0)	Concatenates a sequence of `tensors` along a new dimension (`dim`), all `tensors` must be same size.
torch.squeeze(input)	Squeezes `input` to remove all the dimenions with value `1`.
torch.unsqueeze(input, dim)	Returns `input` with a dimension value of `1` added at `dim`.
torch.permute(input, dims)	Returns a view of the original `input` with its dimensions permuted (rearranged) to `dims`.

creiamo un vettore con 9 valori:

# creo un vettore semplice
import torch
x = torch.arange(1., 10.)
x, x.shape


tensor([1., 2., 3., 4., 5., 6., 7., 8., 9.])

shape -> torch.Size([9])

Reshape

Nell'esempsio voglio convertire il tensore in una matrice di una riga per nove colonne, visto che il numero di elementi è compatibile con l'operazione.

ATTENZIONE che reshape deve essere compatibile con la dimensione.

Quindi:

y = x.reshape(9,1)

y varrà:

tensor([[1.],
         [2.],
         [3.],
         [4.],
         [5.],
         [6.],
         [7.],
         [8.],
         [9.]])

shape -> torch.Size([9, 1])

se inceve volessimo creare un tensore multidimensionale di una riga per nove colonne:

y = x.reshape(1,9)

``` tensor([[1., 2., 3., 4., 5., 6., 7., 8., 9.]])

shape -> torch.Size([1, 9])


##### View

La view è simile a reshape solo che l'output condivide la stessa area di memoria, in pratica modificando uno si modifica anche l'altro, es.

z = x.view(1,9)

\# questo comando modifica la colonna zero di tutte le righe (vale anche se abbiamo una sola riga)

z \[:,0\] = 5

a questo punto sia z che x puntano allo stesso valore (5) nella colonna zero

##### Stack

Concatena due o più tensori purchè abbiano la stessa dimensione e che siano in una lista. (es.

```python
tensor_one = torch.tensor([[1,2,3],[4,5,6]])
print(tensor_one)
tensor([[1, 2, 3],
        [4, 5, 6]])

tensor_two = torch.tensor([[7,8,9],[10,11,12]])
tensor_tre = torch.tensor([[13,14,15],[16,17,18]])

#NB devono essere in una lista es. tensor_list = [tensor_one, tensor_two, tensor_tre] o direttamente come sotto
staked_tensor = torch.stack([tensor_one,tensor_two,tensor_tre])
print(staked_tensor.shape)
torch.Size([3, 2, 3])

print(staked_tensor)
tensor([[[ 1,  2,  3],
         [ 4,  5,  6]],

        [[ 7,  8,  9],
         [10, 11, 12]],

        [[13, 14, 15],
         [16, 17, 18]]])

Squeeze e UnSqueeze

Lo squeeze rimuove tutte le dimensioni "singole" dal tensore, es:

import torch 

# creo un array a (dimensione 0)
xx = torch.arange(1., 10.)
print (xx)
>tensor([1., 2., 3., 4., 5., 6., 7., 8., 9.])


# aggiungo una dimensione (dimensione 1)
xx = xx.reshape(1,9)
print (xx)
>tensor([[1., 2., 3., 4., 5., 6., 7., 8., 9.]])


#tolgo la dimensione che ho aggiunto (solo se dim 1)
print(xx.squeeze())
print (xx)
>tensor([1., 2., 3., 4., 5., 6., 7., 8., 9.])

#Con l'unsqueeze si aggiunga una singola dimensione
print(staked_tensor.squeeze())
>tensor([[[1., 2., 3., 4., 5., 6., 7., 8., 9.]]])

Permute

L'operazione permute permette di "switchare" una dimensione con l'altra, ovvero:

# creiamo un tensore di dimensione 3 di 224 x 224 x 3, che btw potrebbe
# rappresentare un'immagine dove le prime due dimensione sono i pixel mentre la terza il valore RGB
x_original = torch.rand(size=(224, 224, 3))

# la permute lavora per indici, nel caso specifico swppiamo il secondo indice ( è zero based) e lo
# mettimao al primo posto (zero) e così via
x_permuted = x_original.permute(2, 0, 1) # shifts axis 0->1, 1->2, 2->0

print(f"Previous shape: {x_original.shape}")
Previous shape: torch.Size([224, 224, 3])

print(f"New shape: {x_permuted.shape}")
New shape: torch.Size([3, 224, 224])

si noti quindi i valori delle dimensioni vengono "swappati" tra di loro secondo l'ordine definito dal medoto "permute"
ricordarsi inoltre che anche la permute lavora su una vista dei valori originali, con tutto ciò che comporta l'uso di una vista in torch

Indexing

L'indexing è utilizzato per estrapolare, navigare, i dati di un tensore, con pytorch è simile a quello di numpy.

es.

# Creo un tensore

import torch
x = torch.arange(1, 10).reshape(1, 3, 3)
x, x.shape

>tensor([[[1, 2, 3],
          [4, 5, 6],
          [7, 8, 9]]]
        
 >torch.Size([1, 3, 3])
        
# target su primo elemento della matrice tridimensionale
x[0]
>tensor([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])

# target su primo elemento della matrice tridimensionale e di questo elemento il primo
x[0][0]        
>tensor([1, 2, 3])

# target su primo elemento della matrice tridimensionale e di questo elemento il primo e del restante il primo
x[0][0][0]
>1

Selezionare tutti gli elementi di una dimensione

Per selezionare tutti gli elementi di una dimensione bisogna utilizzare il carattere ":"

Per selezionare un'altra dimensione bisogna utilizzare il carattere ","

Ovviamente sono in ordine di dimensione, la prima virgola sarà quella della dimensione zero, la seconda della prima, la terza della seconda e così via.

- per esempio voglio estrarre tutti i valori da tutte le dimensioni zero, il primo valore della dimensione uno.

import torch
x = torch.arange(1, 10).reshape(1, 3, 3)
x, x.shape

>tensor([[[1, 2, 3],
         [4, 5, 6],
         [7, 8, 9]]]) torch.Size([1, 3, 3])
        
        
x[: , 0]

> tensor([[1, 2, 3]])

- tutte le dimensini zero, e uno ma solo gli indice uno della seconda

x[:,:,1]

>tensor([[2, 5, 8]])

- tutti i valori della prima dimensione, ma solo il primo indice della prima e della seconda dimensione

x[:,1,1]

> tensor([5])

- l'indice zero della dimensione zero e delle dimensione uno, e tutti i valori della seconda dimensione

x[0, 0, :] # same as x[0][0]

> tensor([1, 2, 3])

- ritornare il valore '9'

tensor([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])

x[0,2,2]

- ritornare i valori 3,6,9

tensor([[1, 2, 3],
        [4, 5, 6],
        [7, 8, 9]])

x[0,:,2]

oopure

x[:,:,2]

# Create a tensor 
import torch
x = torch.arange(1, 28).reshape(3, 3, 3)
# x, x.shape
print(x)
>tensor([[[ 1,  2,  3],
         [ 4,  5,  6],
         [ 7,  8,  9]],

        [[10, 11, 12],
         [13, 14, 15],
         [16, 17, 18]],

        [[19, 20, 21],
         [22, 23, 24],
         [25, 26, 27]]])
         
print(x[:,0,2])
>tensor([ 3, 12, 21])

Pytorch tensors e Numpy

Numpy è molto utilizzato per elaborare i dati velocemente, accade però che questi dati debbano essere caricati in pytorch per essere dati in pasto alla rete neurale di turno, sia essa nella ram "tradizionale" che quella della GPU.

Un metodo utilizzabile è torch.from_numpy (mdarray) o vice versa torch.Tensor.numpy() es:

``` # da Numpy a tensor

import torch
import numpy as np

array = np.arange (1.0, 8,0) 
tensor = torch.from_numpy (array) 
print (array,tensor)

array([1., 2., 3., 4., 5., 6., 7.]) tensor([1., 2., 3., 4., 5., 6., 7.], dtype=torch.float64)

Attenzione torch converte di defaut in dtype=torch.float64, se invece vogliamo forzare ad un altro tipo es. float32 allora dobbiamo utilizzare il metodo types es: tensor = torch.from_numpy (array).type(torch.float32)




```python
# da Tesor a Numpy
tensor = torch.ones(7)
numpy_tensor = tensor.numpy()

print (array,tensor)

>tensor([1., 1., 1., 1., 1., 1., 1.]),
>array([1., 1., 1., 1., 1., 1., 1.], dtype=float32))

Attenzione in questo caso passiamo da float64 di Torch a float32 di numpy, quindi con possibile perdita di informazioni.

Riproducibilità

Una rete neurale in genere si sviluppa iniziando con valori casuali, poi effettua sempre più operazioni sui tensori che andranno ad aggiornare i numeri, prima casuali, affinandone i volori a quelli utili per lo scopo previsto.

Se desideriamo generare dei numeri "random" che siano sempre gli stessi :) possiamo utilizzare una modalità "random seed" in modo che il caso possa essere riprodotto con gli stessi valori "random" più volte.

import torch
import random

# # Set the random seed
RANDOM_SEED=42 # try changing this to different values and see what happens to the numbers below
torch.manual_seed(seed=RANDOM_SEED) 
random_tensor_C = torch.rand(3, 4)

# Have to reset the seed every time a new rand() is called 
# Without this, tensor_D would be different to tensor_C 
torch.random.manual_seed(seed=RANDOM_SEED) # try commenting this line out and seeing what happens
random_tensor_D = torch.rand(3, 4)

print(f"Tensor C:\n{random_tensor_C}\n")
print(f"Tensor D:\n{random_tensor_D}\n")
print(f"Does Tensor C equal Tensor D? (anywhere)")
print (random_tensor_C == random_tensor_D)

> tensor([[True, True, True, True],
          [True, True, True, True],
          [True, True, True, True]])

Torch on GPU

I tensori e gli oggetti pytorch possono essere eseguiti sia dalla CPU che nella GPU grazie per es. ai CUDA di NVidia.

Per verificare se la GPU è visibile da Torch eseguire il comando:

# Check for GPU
import torch
torch.cuda.is_available()

> true

a questo punto possiamo configurare torch in mode giri nella GPU o nella CPU tramite il comando:

# Set device type
device = "cuda" if torch.cuda.is_available() else "cpu"
some_tensor = some_tensor.to(device)

e vediamo le due possibili casistiche:

# Create tensor (default on CPU)
tensor = torch.tensor([1, 2, 3])

# Tensor not on GPU
print(tensor, tensor.device)
>tensor([1, 2, 3]) cpu

# Move tensor to GPU (if available)
tensor_on_gpu = tensor.to(device)
print (tensor_on_gpu,tensor_on_gpu, tensor_on_gpu.device)
>tensor([1, 2, 3], device='cuda:0') cuda:0

oppure

# creo due tensori random nella GPU
tensor_A = torch.rand(size=(2,3)).to(device)
tensor_B = torch.rand(size=(2,3)).to(device)
tensor_A, tensor_B

se poi vogliamo portare i valori dalla GPU alla GPU dobbiamo fare attenzione in quanto non possiamo semplicemente:

``` # If tensor is on GPU, can't transform it to NumPy (this will error) tensor_on_gpu.numpy()

TypeError Traceback (most recent call last) Cell In[13], line 2 1 # If tensor is on GPU, can't transform it to NumPy (this will error) ----> 2 tensor_on_gpu.numpy()

TypeError: can't convert cuda:0 device type tensor to numpy. Use Tensor.cpu() to copy the tensor to host memory first.


dobbiamo invece:

Instead, copy the tensor back to cpu

tensor_back_on_cpu = tensor_on_gpu.cpu().numpy() print (tensor_back_on_cpu)

array([1, 2, 3], dtype=int64)


##### Esercizi

All of the exercises are focused on practicing the code above.

You should be able to complete them by referencing each section or by following the resource(s) linked.

**Resources:**

- [Exercise template notebook for 00](https://github.com/mrdbourke/pytorch-deep-learning/blob/main/extras/exercises/00_pytorch_fundamentals_exercises.ipynb).
- [Example solutions notebook for 00](https://github.com/mrdbourke/pytorch-deep-learning/blob/main/extras/solutions/00_pytorch_fundamentals_exercise_solutions.ipynb) (try the exercises *before* looking at this).

1. Documentation reading - A big part of deep learning (and learning to code in general) is getting familiar with the documentation of a certain framework you're using. We'll be using the PyTorch documentation a lot throughout the rest of this course. So I'd recommend spending 10-minutes reading the following (it's okay if you don't get some things for now, the focus is not yet full understanding, it's awareness). See the documentation on [`torch.Tensor`](https://pytorch.org/docs/stable/tensors.html#torch-tensor) and for [`torch.cuda`](https://pytorch.org/docs/master/notes/cuda.html#cuda-semantics).
2. Create a random tensor with shape `(7, 7)`.
3. Perform a matrix multiplication on the tensor from 2 with another random tensor with shape `(1, 7)` (hint: you may have to transpose the second tensor).
4. Set the random seed to `0` and do exercises 2 &amp; 3 over again.
5. Speaking of random seeds, we saw how to set it with `torch.manual_seed()` but is there a GPU equivalent? (hint: you'll need to look into the documentation for `torch.cuda` for this one). If there is, set the GPU random seed to `1234`.
6. Create two random tensors of shape `(2, 3)` and send them both to the GPU (you'll need access to a GPU for this). Set `torch.manual_seed(1234)` when creating the tensors (this doesn't have to be the GPU random seed).
7. Perform a matrix multiplication on the tensors you created in 6 (again, you may have to adjust the shapes of one of the tensors).
8. Find the maximum and minimum values of the output of 7.
9. Find the maximum and minimum index values of the output of 7.
10. Make a random tensor with shape `(1, 1, 1, 10)` and then create a new tensor with all the `1` dimensions removed to be left with a tensor of shape `(10)`. Set the seed to `7` when you create it and print out the first te

**Extra-curriculum**

<div class="cell text_cell rendered selected" id="bkmrk-spend-1-hour-going-t" tabindex="2"><div class="inner_cell"><div class="text_cell_render rendered_html" dir="ltr" tabindex="-1">- Spend 1-hour going through the [PyTorch basics tutorial](https://pytorch.org/tutorials/beginner/basics/intro.html) (I'd recommend the [Quickstart](https://pytorch.org/tutorials/beginner/basics/quickstart_tutorial.html) and [Tensors](https://pytorch.org/tutorials/beginner/basics/tensorqs_tutorial.html) sections).
- To learn more on how a tensor can represent data, see this video: [What's a tensor?](https://youtu.be/f5liqUk0ZTw)

</div></div></div>