Multiclass classification
Nella classificazione multipla, a differenza della classificazione binaria possono essere identificate più di due categorie. Importante è comprendere l'utulizzo delle activation functions. Per la multiclass possiamo utilizzare la ReLU o la Sigmoid.
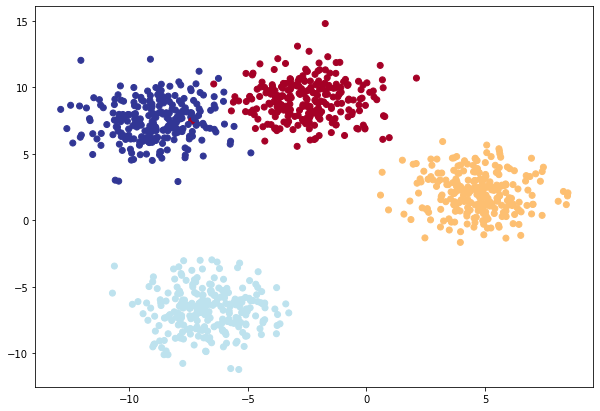
Per esempio voglio classificare 4 classi di "blobs" :) lol come nell'immagine sotto riportata, utilizzando il pacchetto sklearn:
from sklearn.datasets import make_blobsIl modello
costruisco il modello per la gestione della classificazione multipla:
class BlobModel(nn.Module): # la nn.Module è la superclasse da derivare per costruire un modello
# customizzo gli input al costruttore
def __init__(self, input_features, output_features, hidden_units=8):
"""Initializes all required hyperparameters for a multi-class classification model.
Args:
input_features (int): Number of input features to the model.
out_features (int): Number of output features of the model
(how many classes there are).
hidden_units (int): Number of hidden units between layers, default 8.
"""
super().__init__()
# definisco i layers e il numero di neuroni che li compongnono.
# NB: i layer sono lineari e quindi rispondono all'equazione y = xw+b
self.linear_layer_stack = nn.Sequential(
nn.Linear(in_features=input_features, out_features=hidden_units),
nn.ReLU(), # <- does our dataset require non-linear layers? (try uncommenting and see if the results change)
nn.Linear(in_features=hidden_units, out_features=hidden_units),
nn.ReLU(), # <- does our dataset require non-linear layers? (try uncommenting and see if the results change)
nn.Linear(in_features=hidden_units, out_features=output_features), # how many classes are there?
)
def forward(self, x):
return self.linear_layer_stack(x)Da notare che l'ultimo livello della rete neurale, (l'output level) è composto da tanti neuroni quante sono le classi da classificare. Ciascun neurone di output è associato ad una classe e ne rappresenta la probabilità che l'intput appartenga ad a Niesima classe.
NB: ricordo che i livelli sono "lineari", il che significa che corrispondono all'equazione y=x⋅WeightsT+bias il che significa bisogna aggiungere delle funzioni non lineari in grado di "spezzare" le equazioni lineari. Potremmo inserire, tra un livello lineare e l'altro una funzion non lineare come la ReLU.
Ovvimante se i dati sono nettamente separati e quindi una linea retta li può "dividere" allora potremmo evitare di inserire le funzioni di attivazione non lineare. Nell'esempio sopra visabile i 4 gruppi di "blobs" possono essere appunto separati da linee rette, il modello potrà quindi anche (opzionale) non utilizzare le ReLU non lineari.
Per le funzioni di attivazione non lienari vedi:
La loss function
Per la classificazione multiclasse andiamo a vedere cosa pytorch offre nella pagina Loss functions
Per la binary classification in genere si usa la nn.BCEWithLogitsLoss mentre per la multiclassification si usa la nn.CrossEntropyLoss
TIP: Per la CrossEntropy fare attenzione al parametro "weight " da valorizzare nel caso i cui il numero di elementi delle classi sono diversi tra di loro, es. i gialli sono 100 metre i versi sono 20...
loss_fn = nn.CrossEntropyLoss()L'Optimizer
Come ottimizer possiamo utilizzare quelli generici come l'Adam o il pià classico SGD, vedi pagina optimezers.
optimizer = torch.optim.SGD(model_4.parameters(), lr=0.1)Il training loop
# Fit the model
torch.manual_seed(42)
# Set number of epochs
epochs = 100
# looppo..
for epoch in range(epochs):
### Training
model_4.train()
# 1. Forward pass
y_logits = model_4(X_blob_train) # model outputs raw logits
y_pred = torch.softmax(y_logits, dim=1).argmax(dim=1) # go from logits -> prediction probabilities -> prediction labels
# print(y_logits)
# 2. Calculate loss and accuracy
loss = loss_fn(y_logits, y_blob_train)
acc = accuracy_fn(y_true=y_blob_train,
y_pred=y_pred)
# 3. Optimizer zero grad
optimizer.zero_grad()
# 4. Loss backwards
loss.backward()
# 5. Optimizer step
optimizer.step()
### Testing
model_4.eval()
with torch.inference_mode():
# 1. Forward pass
test_logits = model_4(X_blob_test)
# NB: i logits vengono passati alla funzione softmax che restituisce la probabilità
# che un valore del vettori si verifichi... (un po' forzato ma spero renda l'idea)
test_pred = torch.softmax(test_logits, dim=1).argmax(dim=1)
# 2. Calculate test loss and accuracy
test_loss = loss_fn(test_logits, y_blob_test)
test_acc = accuracy_fn(y_true=y_blob_test,
y_pred=test_pred)
# Print out what's happening
if epoch % 10 == 0:
print(f"Epoch: {epoch} | Loss: {loss:.5f}, Acc: {acc:.2f}% | Test Loss: {test_loss:.5f}, Test Acc: {test_acc:.2f}%")Importante capire il funzionamento della softmax alla quale verranno passati i logits. Per comprendere meglio la softmax vedi link.
La classe completa:
# Import dependencies
import torch
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from torch import nn
import numpy as np
# Set the hyperparameters for data creation
NUM_CLASSES = 4
NUM_FEATURES = 2
RANDOM_SEED = 42
# 1. Create multi-class data
X_blob, y_blob = make_blobs(n_samples=1000,
n_features=NUM_FEATURES, # X features
centers=NUM_CLASSES, # y labels
cluster_std=1.5, # give the clusters a little shake up (try changing this to 1.0, the default)
random_state=RANDOM_SEED
)
# 2. Turn data into tensors
X_blob = torch.from_numpy(X_blob).type(torch.float)
y_blob = torch.from_numpy(y_blob).type(torch.LongTensor)
print(X_blob[:5], y_blob[:5])
# 3. Split into train and test sets
X_blob_train, X_blob_test, y_blob_train, y_blob_test = train_test_split(X_blob,
y_blob,
test_size=0.2,
random_state=RANDOM_SEED
)
# 4. Plot data
# plt.figure(figsize=(10, 7))
# plt.scatter(X_blob[:, 0], X_blob[:, 1], c=y_blob, cmap=plt.cm.RdYlBu);
# Calculate accuracy (a classification metric)
def accuracy_fn(y_true, y_pred):
correct = torch.eq(y_true, y_pred).sum().item() # torch.eq() calculates where two tensors are equal
acc = (correct / len(y_pred)) * 100
return acc
def plot_decision_boundary(model: torch.nn.Module, X: torch.Tensor, y: torch.Tensor):
"""Plots decision boundaries of model predicting on X in comparison to y.
Source - https://madewithml.com/courses/foundations/neural-networks/ (with modifications)
"""
# Put everything to CPU (works better with NumPy + Matplotlib)
model.to("cpu")
X, y = X.to("cpu"), y.to("cpu")
# Setup prediction boundaries and grid
x_min, x_max = X[:, 0].min() - 0.1, X[:, 0].max() + 0.1
y_min, y_max = X[:, 1].min() - 0.1, X[:, 1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 101), np.linspace(y_min, y_max, 101))
# Make features
X_to_pred_on = torch.from_numpy(np.column_stack((xx.ravel(), yy.ravel()))).float()
# Make predictions
model.eval()
with torch.inference_mode():
y_logits = model(X_to_pred_on)
# Test for multi-class or binary and adjust logits to prediction labels
if len(torch.unique(y)) > 2:
y_pred = torch.softmax(y_logits, dim=1).argmax(dim=1) # mutli-class
else:
y_pred = torch.round(torch.sigmoid(y_logits)) # binary
# Reshape preds and plot
y_pred = y_pred.reshape(xx.shape).detach().numpy()
plt.contourf(xx, yy, y_pred, cmap=plt.cm.RdYlBu, alpha=0.7)
plt.scatter(X[:, 0], X[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
# creiamo il modello
class BlobModel(nn.Module): # la nn.Module è la superclasse da derivare per costruire un modello
# customizzo gli input al costruttore
def __init__(self, input_features, output_features, hidden_units=8):
"""Initializes all required hyperparameters for a multi-class classification model.
Args:
input_features (int): Number of input features to the model.
out_features (int): Number of output features of the model
(how many classes there are).
hidden_units (int): Number of hidden units between layers, default 8.
"""
super().__init__()
# definisco i layers e il numero di neuroni che li compongnono.
# NB: i layer sono lineari e quindi rispondono all'equazione y = xw+b
self.linear_layer_stack = nn.Sequential(
nn.Linear(in_features=input_features, out_features=hidden_units),
# nn.ReLU(), # <- does our dataset require non-linear layers? (try uncommenting and see if the results change)
nn.Linear(in_features=hidden_units, out_features=hidden_units),
# nn.ReLU(), # <- does our dataset require non-linear layers? (try uncommenting and see if the results change)
nn.Linear(in_features=hidden_units, out_features=output_features), # how many classes are there?
)
def forward(self, x):
return self.linear_layer_stack(x)
# Create an instance of BlobModel and send it to the target device
model_4 = BlobModel(input_features=NUM_FEATURES,
output_features=NUM_CLASSES,
hidden_units=8)
# Create loss and optimizer
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model_4.parameters(),
lr=0.1) # exercise: try changing the learning rate here and seeing what happens to the model's performance
# Fit the model
torch.manual_seed(42)
# Set number of epochs
epochs = 100
# Put data to target device
for epoch in range(epochs):
### Training
model_4.train()
# 1. Forward pass
y_logits = model_4(X_blob_train) # model outputs raw logits
y_pred = torch.softmax(y_logits, dim=1).argmax(dim=1) # go from logits -> prediction probabilities -> prediction labels
# print(y_logits)
# 2. Calculate loss and accuracy
loss = loss_fn(y_logits, y_blob_train)
acc = accuracy_fn(y_true=y_blob_train,
y_pred=y_pred)
# 3. Optimizer zero grad
optimizer.zero_grad()
# 4. Loss backwards
loss.backward()
# 5. Optimizer step
optimizer.step()
### Testing
model_4.eval()
# setto l'inference il che sta a indicare che voglio testare il modello per fare delle previsioni
with torch.inference_mode():
# 1. Forward pass
test_logits = model_4(X_blob_test)
test_pred = torch.softmax(test_logits, dim=1).argmax(dim=1)
# 2. Calculate test loss and accuracy
test_loss = loss_fn(test_logits, y_blob_test)
test_acc = accuracy_fn(y_true=y_blob_test,
y_pred=test_pred)
# Print out what's happening
if epoch % 10 == 0:
print(f"Epoch: {epoch} | Loss: {loss:.5f}, Acc: {acc:.2f}% | Test Loss: {test_loss:.5f}, Test Acc: {test_acc:.2f}%")
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.title("Train")
plot_decision_boundary(model_4, X_blob_train, y_blob_train)
plt.subplot(1, 2, 2)
plt.title("Test")
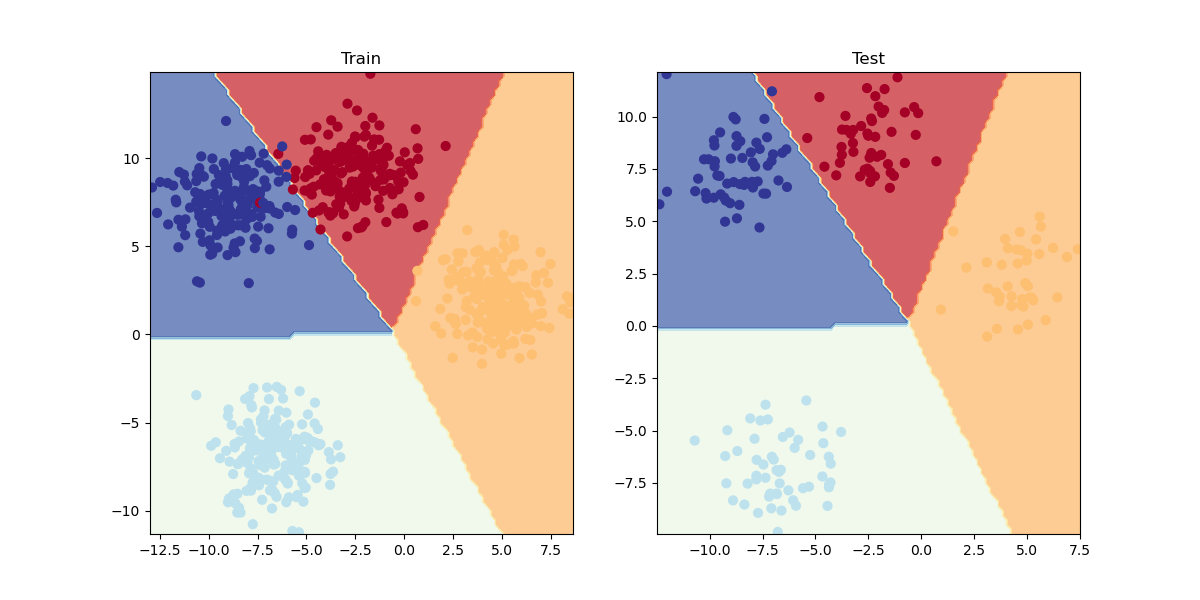
plot_decision_boundary(model_4, X_blob_test, y_blob_test)Il cui output sarà:
da notare che vista la distribuzioni dei "blobs" non è necessario utilizzare funzioni non lineare come la ReLU, questo perchè i dati dei blobs sono "separabili linearmente", il che significa che i dati dei blobs non si michiano in maniera non lineare come per es. nel caso di due cerchi concentrici di blobs.
Il cui output è:
Python 3.10.8 | packaged by conda-forge | (main, Nov 24 2022, 14:07:00) [MSC v.1916 64 bit (AMD64)]
Type 'copyright', 'credits' or 'license' for more information
IPython 8.7.0 -- An enhanced Interactive Python. Type '?' for help.
PyDev console: using IPython 8.7.0
Python 3.10.8 | packaged by conda-forge | (main, Nov 24 2022, 14:07:00) [MSC v.1916 64 bit (AMD64)] on win32
runfile('C:\\lavori\\formazione_py\\src\\formazione\\DanielBourkePytorch\\03_multiclass_classification.py', wdir='C:\\lavori\\formazione_py\\src\\formazione\\DanielBourkePytorch')
tensor([[-8.4134, 6.9352],
[-5.7665, -6.4312],
[-6.0421, -6.7661],
[ 3.9508, 0.6984],
[ 4.2505, -0.2815]]) tensor([3, 2, 2, 1, 1])
Epoch: 0 | Loss: 1.42610, Acc: 24.12% | Test Loss: 1.14118, Test Acc: 55.00%
Epoch: 10 | Loss: 0.69430, Acc: 71.25% | Test Loss: 0.59211, Test Acc: 78.00%
Epoch: 20 | Loss: 0.54481, Acc: 72.88% | Test Loss: 0.45338, Test Acc: 79.50%
Epoch: 30 | Loss: 0.46979, Acc: 73.12% | Test Loss: 0.38420, Test Acc: 79.00%
Epoch: 40 | Loss: 0.43818, Acc: 73.12% | Test Loss: 0.35307, Test Acc: 79.00%
Epoch: 50 | Loss: 0.42259, Acc: 77.38% | Test Loss: 0.33220, Test Acc: 93.00%
Epoch: 60 | Loss: 0.12337, Acc: 99.00% | Test Loss: 0.09245, Test Acc: 99.50%
Epoch: 70 | Loss: 0.06762, Acc: 99.00% | Test Loss: 0.05245, Test Acc: 99.50%
Epoch: 80 | Loss: 0.05137, Acc: 99.00% | Test Loss: 0.03963, Test Acc: 99.50%
Epoch: 90 | Loss: 0.04380, Acc: 99.12% | Test Loss: 0.03331, Test Acc: 99.50%
Backend MacOSX is interactive backend. Turning interactive mode on.