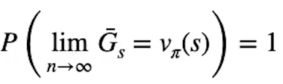Sessione 3 (Metodo Montecarlo)

Il Metodo Montecarlo (MC) migliora la policy iteragendo con l'ambiente e ottenendo dei ritorni (scantati da gamma) di cui viene calcolata la media. Per  la legge dei grandi numeri più osservazioni (e quindi ritorni) otteniamo più ci avviciniamo al valore ottimale atteso Vπ(S). 

Dalla formula si evince che il limite per n che tende a infinto dove n è il numero di misurazioni, genera una stima dei valori degli stati con probabilià 100% di essere ottimale.

Il MC ha dei vantaggi rispetto al DP (dynamic programmig spiegata nella sessione 2):

• la stima dei valori degli stati non dipende dagli altri
• il costo per stimare il valore di uno stato è indipendente dal numero toale degli stati

Nel caso del DP l'algoritmo bootstrappa il valore degli altri stati in modo da utilizzare una stima per produrne un'altra. Per questo la complessità di un algoritmo cresce esponenzialmente con il numero di stati.

Cosa molto importante MD non necessita del modello, la dinamica dell'ambiete sarà implicita nella nostra stima.

Per risolvere l'algorimo del MC verrà utilizzato il metodo, visto in precedenza anche con il DP detto "Generalized Policy Iteration".

 

Generalized Policy Iteration

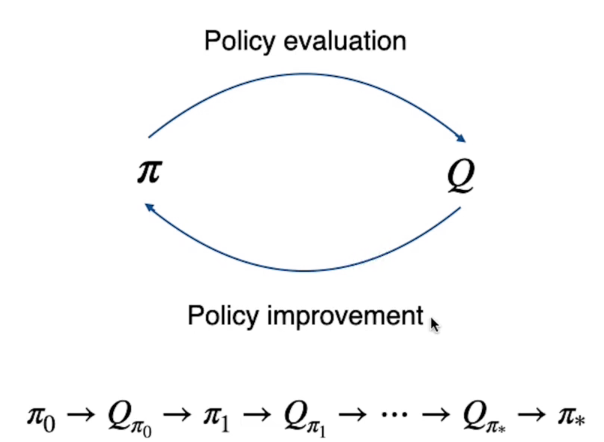
La GPI si basa sulla valutazione della policy (partendo da una che può essere randomica o arbitraria) per poi migliorarla e looppando fino a quando non si arriva a quella ottiamale.

 

MC si elabora generando un episodio la cui traiettoria parte dallo stato iniziale sino allo stato finale durante il qualche vengono raccolte e sommate tutte le ricompense scontate gamma, per ogni stato dell'enviroment.

Bisogna quindi trovare la policy che sceglie l'azione con il Q-Value più alto, nella pratica dovremo tenere traccia nella tabella dei valori, non più i valori degli stati V(s) come nel DP, ma salveremo i valori delle azioni Q(s,a), ovvero dell'azione che massimizza il valore.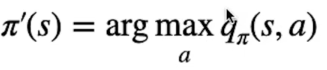

Il processo per MC diventerà quindi:

Dove la policy calcola i Q-Value  che viene a sua volta utilizzato per migliorare la policy in un ciclo continuo fino ai valori ottimali Q* e π*.

Exploration

Quindi la policy migliora sulla base dell'esperienza che agente effettua mentre interagisce con l'ambiente. L'esperienza che l'agente raccoglie dipende dalle azioni che l'agente effettua, e le azioni dipendono dalla policy che l'agente utilizza in quel momento. Per questo motivo avremo una policy π' che seleziona l'azione sulla base delle stime Q(s,a). E queste stime saranno sempre più accurate soprattutto mentre ci avviciniamo alle fasi finali dell'apprendimento. (a differenza delle fase iniziale dove invece sono inaccurate)

Immaginiamo il caso in cui l'azione è ottimale ma la sua stima Q(s,a) è pessima, allora la policy non la sceglierà in quanto la stima del valore è molto bassa. Si rende quindi necessario che tutte le azioni vengano scelte ogni tanto in maniera casuale per "esplorare" l'ambiente con scelte che normalmente non verrebbero effettuate, ma che possono migliorare la policy anche se apparentemente non nell'immediato. Tutto questo per scoprire eventuali azioni ottimali non considerate dalla policy in uso.

Quindi come mantenere l'esplorazione?

Beh, nella pratica abbiamo due opzioni:

1. La prima si chiama "exploring starts" e prevede che l'agente inizi la sua esplorazione in uno stato casuale dell'ambiente ed effettui un'azione iniziale casuale. Purtroppo non è una modalità molto realistica in quanto ci sono molti task che semplicamente non hanno questa possibilità. (soprattutto se parliamo del mondo reale)
2. La seconda si chiama "stocastic policies" ovvero vengono considerate le azioni che hanno una probabilità maggiore di zero, in questo modo ogni tanto vengono prese delle azioni "a caso" che potrebbero aiutare la policy a migliorare grazie al caso. (una sorta di evoluzione naturale della specie :) ) Queta seconda ipotesti è più realista e più facilmente implementabil.

Le policy stocastiche si suddivino in due tipologie:

• On-policy learning strategies: la quale genera l'esperienza basandosi nulla stessa policy che stiamo ottimizzando
• Off-policy learning strategies: la quale utilizza due policy distinte, una per esplorare l'ambiente e un'altra da ottimizzare

On-policy

42