Sessione 2

Model-free control (Monte Carlo e Temporal difference)

Nel capitolo precedente abbiamo svolto un lavoro di pianificazione e non di appredimento per rinforzo in quanto avevamo il modello (ambiente) che ci diceva con quale probabilità svolgeva le azioni. La policy (pi) era in qualche modo nota, questo però non rappresenta la realtà in quanto il modello, nella natura delle cose, non ci viene dato apriori, dobbiamo quindi trovare un modo per ricavarlo, come fare? Bene bisogna quindi interrogare l'ambiete e con le risposte ottenute ricavare in quale modo il modello. 

Si deve quindi fare un lavoro di predizione e di miglioramento del modello (policy)

Predizione

E' model free perchè non abbiamo a priori il modello, cosa che invece avevamo all'inizio del corso con la pianificazione.

Dobbiamo quindi fare un lavoro di predizione che si basa su due modalità:

1) il primo metodo è detto Monte Carlo (MC), nella pratica voglio "imparare" il valore delle mie azioni iteragendo con l'ambiente. Svolgo quindi un episodio partendo dallo stato k e raccolgo tutti i valori, e relative reward, degli stati fino allo stato terminale, faccio la media aritmetica G(T) e salvo il valore ottenuto nello stato k. Svolgo questo lavoro per N volte per tutti gli M stati, in questo modo a tendere, sempre per la legge dei grandi numeri, mi avvicino al valore reale dello stato. (da notere che con questo metodo non devo inizializzare gli stati in quanto interrogo subito l'ambiente)

2) il secondo metodo, detto anche Temporal difference (TD). E' un metodo iterativo, per prima cosa devi inizializzare tutti gli stati con dei valori che potrebbero anche essere random. Partendo dallo stao k faccio una sola azione per arrivare nello stato k+1 e raccolgo il valore dello stato e la rimpensa corrispondente all'azione. Torno quindi allo stato in cui ero parito (k) e aggiorno il valore. Come aggiorno il valore di K? V(k) = V(k) + alpha(R + V(k+1) - Vk) dove aplha è il fattore di apprendimento, più è grande più do importanza al valore restituito dallo stato k+1. Che significa sommare il valore dello stato attuale alla somma data dalla reward più la differenza tra il valore dello stato successivo e il valore dello stato attuale, il tutto moltiplicato per il tasso di apprendimento alpha. Da notare che la differenza tra V(k) e alpha(R + V(k+1) - Vk) è detta errore, che posso variare con il tasso di apprendimento alpha.  Poi si continua passando allo stato successvo e faccio la stessa cosa aggiornando V(k+1) con i valori ricavati da V(k+2). Anche quindi come con il MC faccio passare tutti gli stati M e lo faccio per N volte, in questo modo i valori a tendere (dopo un numero considerevole di volte) convergeranno al valore reale.

Miglioramento e controllo

Nella predizione, viene sempre applicata la stessa policy, ovvamente anche la policy deve migliorare nel tempo, ecco che quindi dopo il ciclo di predizione deve seguire il ciclo di miglioramentento e controllo della policy. Questo significa che i valori  degli stati migliorarano nella fase di predizione e che la scelta degli stati stessi, conseguenza del miglioramento della policy, cambia in quanto le azioni cambiano (in genere) con il cambio della policy per via del miglioramento della stessa.

Esistono due famiglie di metodi me fare miglioramento e controllo e sono relative ai due metodi visti per fare predizione, e sono:

1) On-policy MC control

2) On-policy TD control

3) Off-policy prediction

4) Off-policy control

Che differenza c'è tra i metodi on-policy e off-policy?

On-policy

Questi metodi nella pratica utilizzano la stessa policy migliorandola. Ovvero agendo "greedy" vengono scelte le azioni che massimizzano il risultato e che ne migliorarno la polcy, ma, la policy seppur migliorata è sempre la stessa.

Off-policy

Con i metodi off-policy viene introdotto un fattore di "esplorazione" che in qualche modo crea delle policy nuove "parallele" a quella che stiamo migliorando, per poi metterle in qualche modo a confronto ed eventualmente cambiare la policy con quella nuova trovata tramite esplorazione.

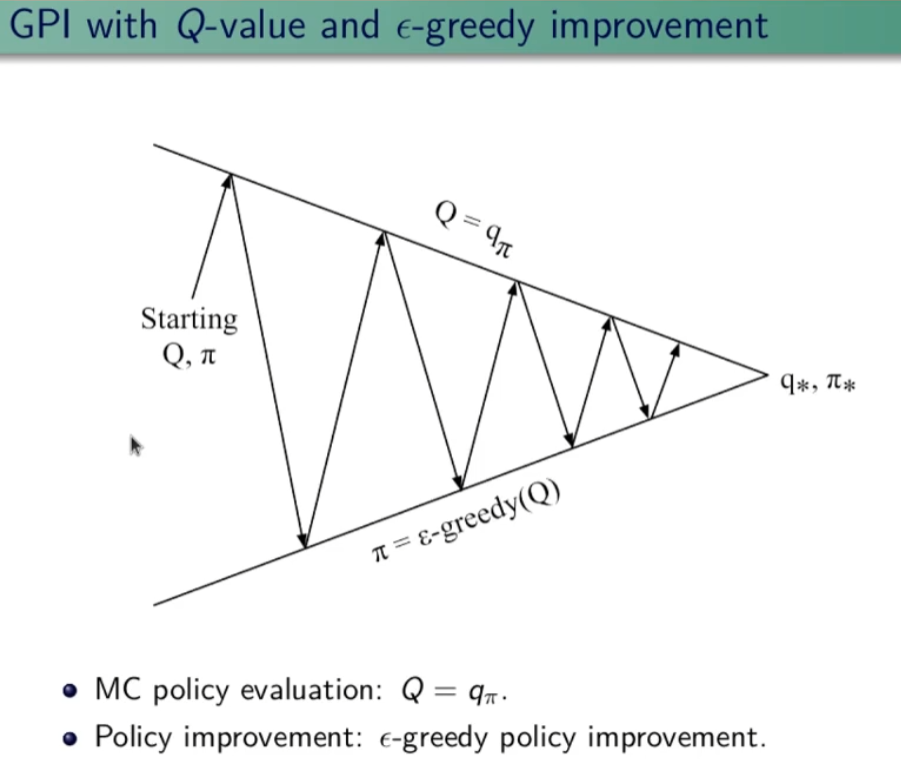
General Policy Iteration

Come miglioro la policy? Basta fare il calcolo della funzione valore stato-azione Q(s,a) anzichè il valore della stato azione V(s) in modo da ottere la probabilità dell'azione. Ok, ma questo non serve realmente per migliorare la policy in quanto agisce sempre in manidera greedy sulla stessa policy. Per migliorare la policy quindi è necessario scegliere "ogni tanto" delle azioni che non sono greedy in modo da effettuare l'esplorazione.

Di qui il metodo "epsisol greedy" (ε-greedy) , dove epsilon è la percentuale di scelta di una azione casuale. (in genere un valore piccolo es. 10%)