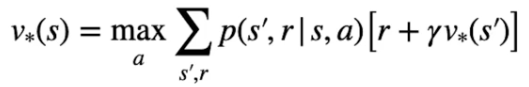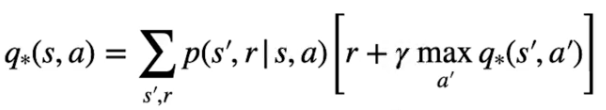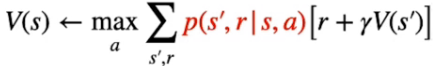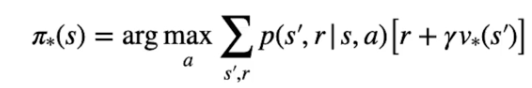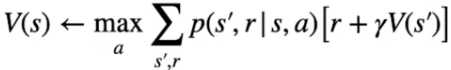Sessione 2 (Dynamic Programming)

La programmazione dinamica (aka DP) è il primo metodo in grado di risolvere il task di controllo.

Lo scopo del DP è tovare la policy ottimale π* per ogni stato V dell'ambiente (che nel nostro caso è discreto)

Per determinare quindi la policy ottimale bisogna rispettare la catena di dipendenze tra stato-azione e stato-valore, ovvero:

Nella pratica l'equazione di Bellman si dettagglia, nel caso di V* come il valore ottimable ricavato dal'azione che lo massimizza, ovvero:

e nel caso dello stato azione come la probabilità più alta che massimizzi di ritorno:

Partiamo dallo stato valore, per poter tovare il valore ottimale bisogna inzializzare tutti gli stati con dei valori a piacere, poi attraverso un processo detto di "sweep" gli stati subiscono una serie di "passate" che ne affina man mano i valori fino a farli convergere verso l'ottimo. Ogni volta che quindi aggiorniamo i valori stimati andiamo a migliorarli e per questo la nuova stima sarà megliore della precedente.

NOTA: uno dei problemi del DP è che necessita di un "modello perfetto" che descriva con precisione la transizione da uno stato all'altro, cosa che in genere non avviene nella realtà. Il modello perfetto ritorna quindi le probabilità di transizione degli stati, come evidenziato nella parte rossa della formula sotto riportata:

Un dei limiti che del DP è che parte dal presupposto che si conosca il modello e che quindi se ne possa verificare con esattezza il comportamento e quindi i ritorni. Nella realtà non è possibile fare questo, serviranno altri metodi che analizzano il comportamento dell'ambiente e cercano di stimare un modello.

Iterazione del valore

Ora vediamo l'algoritmo di "iterazione del valore" utile per determinare la policy ottimale π*. Tale algoritmo calcolo lo stato valore ottimale attraverso N passate (dette anche sweep)

Questa policy fa in modo che per ciascuno stato venga eseguita l'azione che massimizza il ritorno. Per trovare l'azione migliore dobbiamo però conoscere il valore ottimale dello stato che potrebbe seguire lo stato attuale. Per determinare il valore ottimale dobbiamo implementare un processo iterativo sugli stati, per far questo manterremo una tabella con i valori stimati per ciascuno stato. L'inizializzazione iniziale non deve essere suibito ottimale, può anche contenere valori randomici che attraverso le varie passate (sweeps) migliorano convergendo all'ottimale.

La reqola di aggiornamento degli stati sarà quindi:

Formula che tradotta significa: determinare l'azione con la probabilità più alta di ottenere la reward che massimizza il ritorno  per andare dallo stato s allo stato s'.

Di seguito lo pseudo codice che determina la policy ottimale attraverso la massimizzazioni degli stati valore:

Come si può vedere si tratta due due cicli innestati, il primo che looppa fino a che il valore precedente di ciascun stato si avvicina al valore attuale, il che significa che lo stato valore non sta migliorando più di tanto e quindi possiamo assumere una convergenza.

Il secondo loop, fa passare tutti gli stati dell'ambiente e per ciascun stato calcola l'equazione di bellman assumento  una policy di default che assegna la stessa probabilità per ciascuna azione. In questo modo a tendere alcune di queste probabilità, pur essendo uguali, andranno a trovare il ritono migliore.

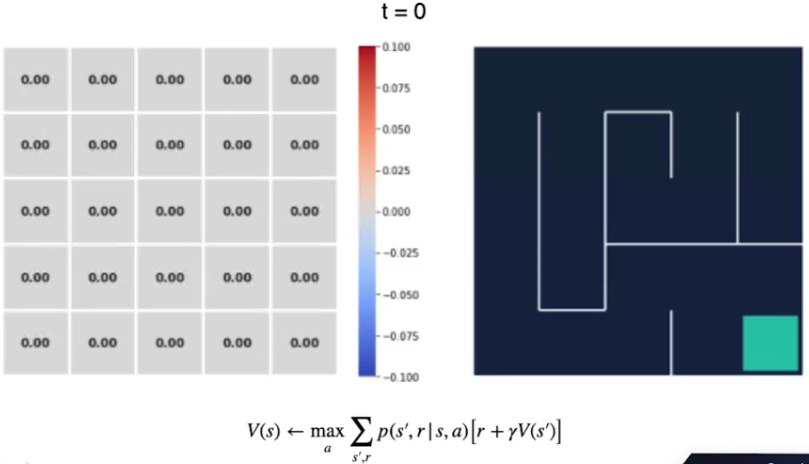
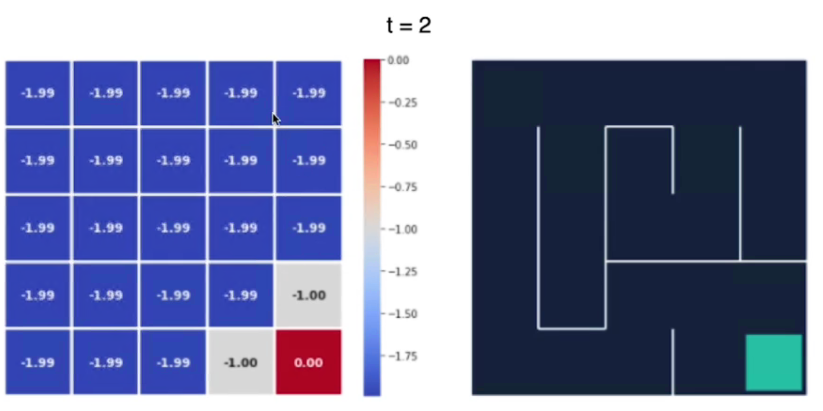
Vediamo con un esempio, qui abbiamo il labirinto di 5x5 al tempo t0 i cui valori degli stati sono inizializzati a zero. (sebbene avremmo potuto scegliere altri valori anche random)

La ricompensa per ogni azione è -1 tranne che per lo stato finale che è pari a zero.

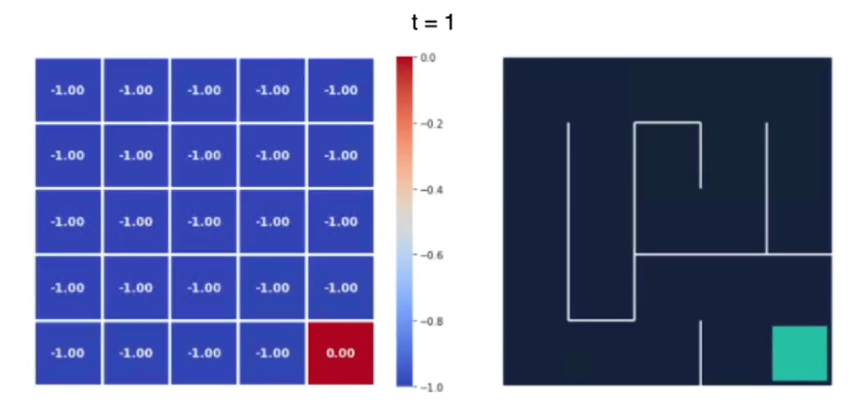
Quindi iniziamo a iterare su tutti gli stati fino all'ultimo che è quello finale, al tempo t1 il valore degli stati sarà:

si può notare come le ricompense sono tutte -1 tranne lo stato goal finale.

Al tempo t2 notiamo che il valore degli stati si "propaga" dallo stato goal a quello successivo:

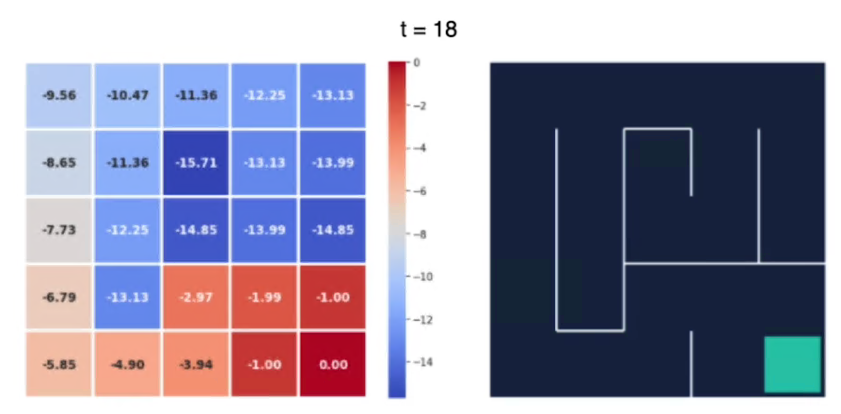
e alla fine dopo 18 iterazioni abbiamo i valori non cambiano in maniera sostanziali, siamo quindi arrivati vicini al valore ottimale:

Possiamo notare che più siamo lontani dal goal e più è basso il valore dello stato.

L'agente raccoglie più ricompense negative quando è più lontano dal goal, invece più il percorso che lo porta al goal è breve, meno saranno le ricompense negative che verrano assegnate allo stao.

Per esempio il valore -15,71 è il più alto perchè da quello stato il percorso per arrivare al goal è il più lungo.

26