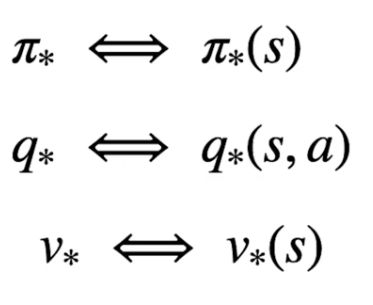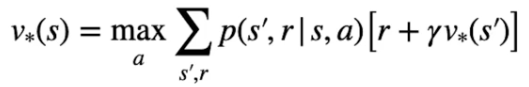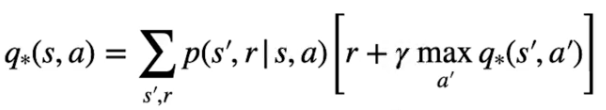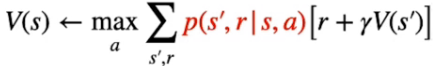Sessione 2 (Dynamic Programming)

La programmazione dinamica (aka DP) è il primo metodo in grado di risolvere il task di controllo.

Lo scopo del DP è tovare la policy ottimale π* per ogni stato V dell'ambiente (che nel nostro caso è discreto)

Per determinare quindi la policy ottimale bisogna rispettare la catena di dipendenze tra stato-azione e stato-valore, ovvero:

Nella pratica l'equazione di Bellman si dettagglia, nel caso di V* come il valore ottimable ricavato dal'azione che lo massimizza, ovvero:

e nel caso dello stato azione come la probabilità più alta che massimizzi di ritorno:

Partiamo dallo stato valore, per poter tovare il valore ottimale bisogna inzializzare tutti gli stati con dei valori a piacere, poi attraverso un processo detto di "sweep" gli stati subiscono una serie di "passate" che ne affina man mano i valori fino a farli convergere verso l'ottimo. Ogni volta che quindi aggiorniamo i valori stimati andiamo a migliorarli e per questo la nuova stima sarà megliore della precedente.

NOTA: uno dei problemi del DP è che necessita di un "modello perfetto" che descriva con precisione la transizione da uno stato all'altro, cosa che in genere non avviene nella realtà. Il modello perfetto ritorna quindi le probabilità di transizione degli stati, come evidenziato nella parte rossa della formula sotto riportata:

Un dei limiti che del DP è che parte dal presupposto che si conosca il modello e che quindi se ne possa verificare con esattezza il comportamento e quindi i ritorni. Nella realtà non è possibile fare questo, serviranno altri metodi che analizzano il comportamento dell'ambiente e cercano di stimare un modello.

24