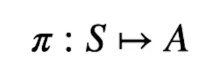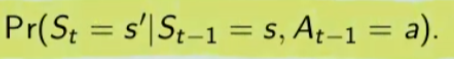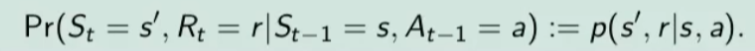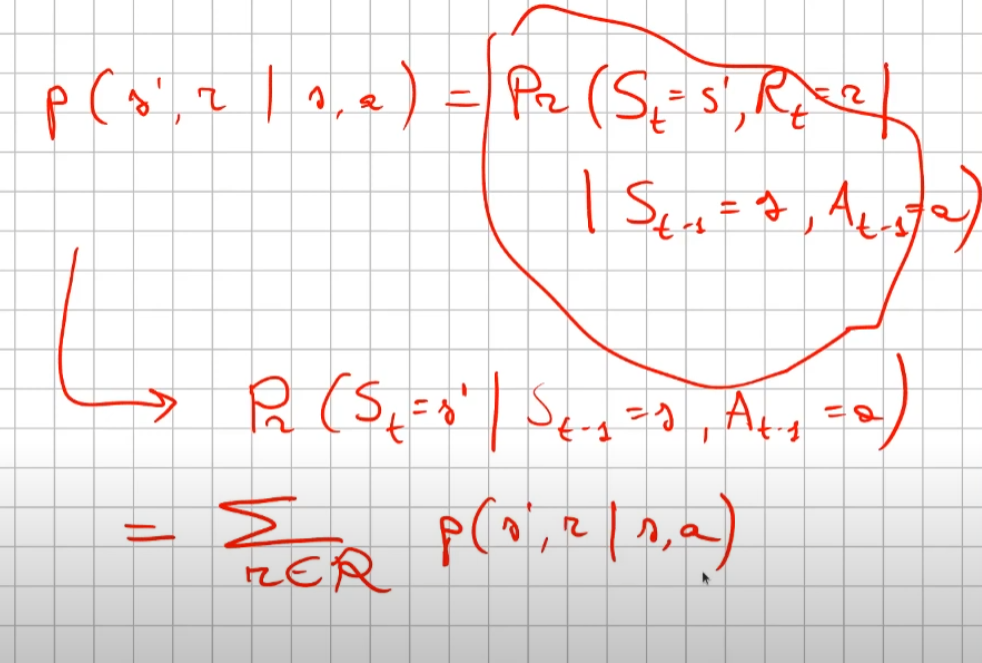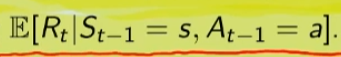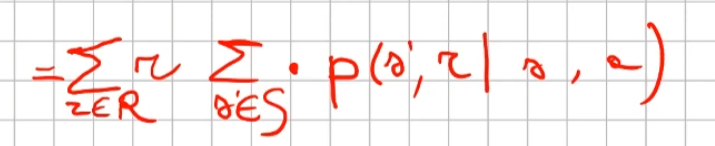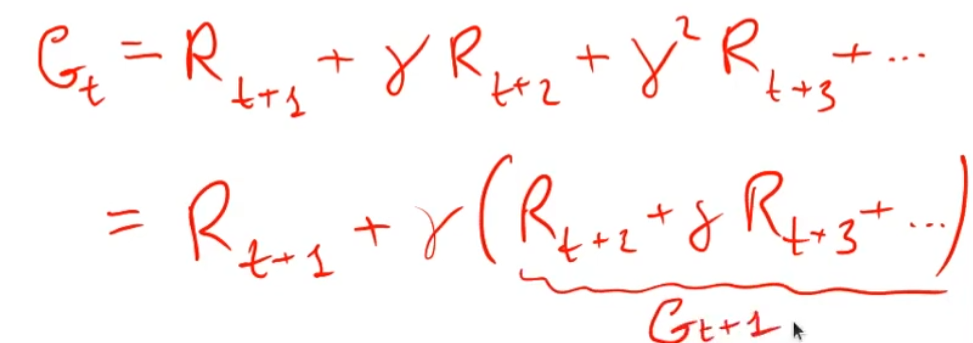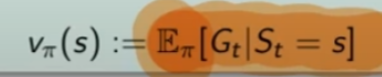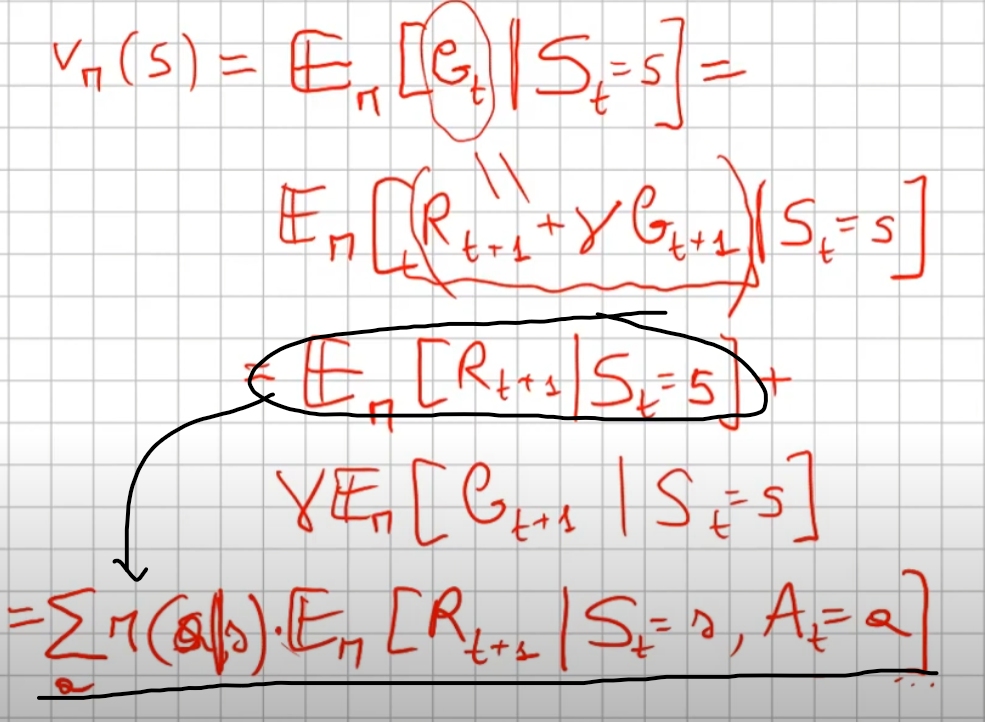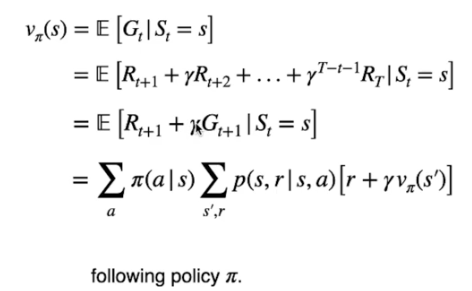Le basi

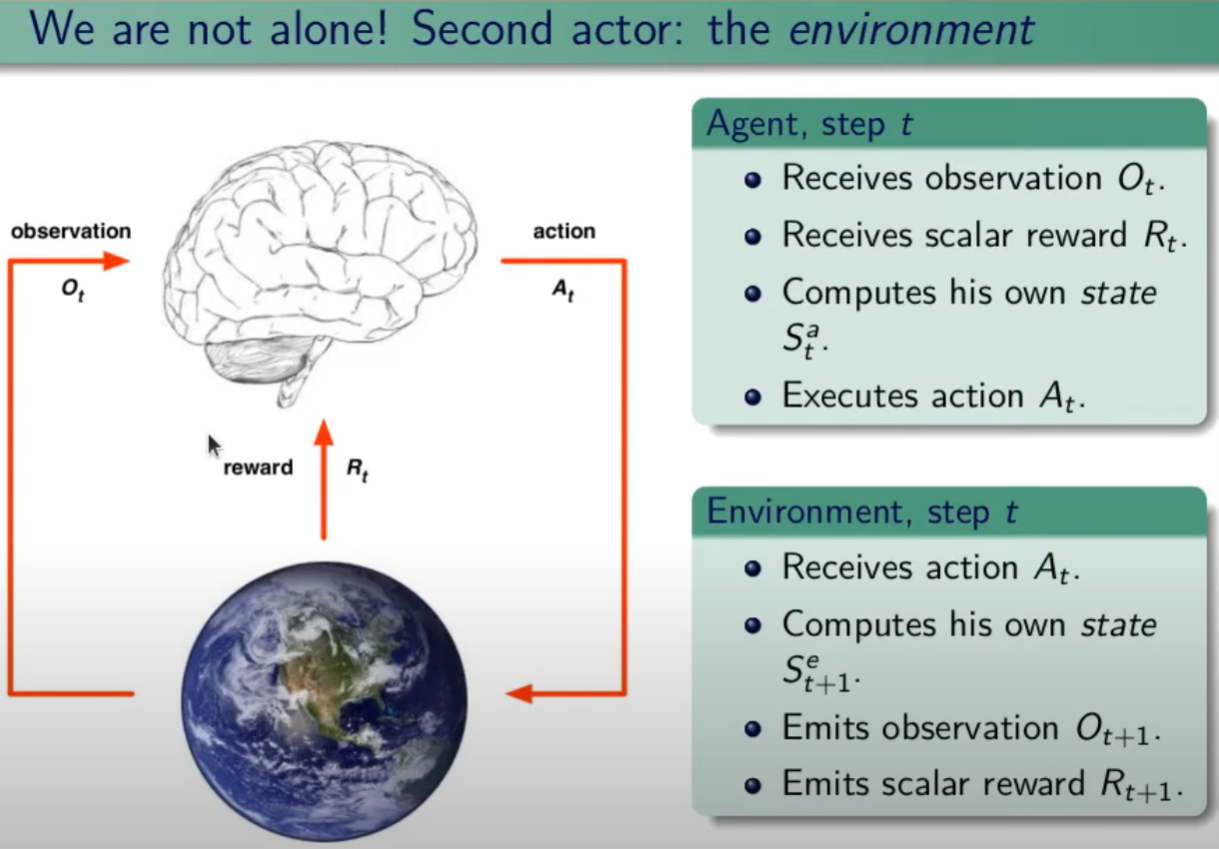
Nell'apprendimento per rinforzo (d'ora in poi verrà indicato con RL) si basa sul processo decisionale di Markov aka MDP attrraverso un task di controllo dove un set di possibili stati e azioni ritornano un reward e una probabilità di passaggio ad uno stato all'altro. Il task nella pratica è un "compito" o una simulazione che per essere svolta (risolta) implica l'utilizzo dell'MDP.

NB: Il processo decisionale di Markov (MDP) asserisce che il passaggio allo stato successivo T+1, dipende esclusivamente dallo stato attuale T e non dagli stati precedenti. Quindi il processo NON ha memoria.

Tipologie di processi decisionali di Markov

Esistono due tipologie di MPD, il processo a stati finiti e quello a stati infiniti.

Nel MDP finiti gli stati finiti hanno un numero finiti di stati definiti dall'ambiente, es. l'uscita da un labirinto di 5 caselle x 5. In questo caso abbiamo 25 stati e 4 azioni (su, giù, dx e sx)

Nel MDP a stati infiniti, invece, l'ambiente appunto può restituire infiniti stati a fronte di infinite azioni, pensiamo per es. il sistema di guida automatica di una macchina dove l'azione es. girare il volante, è un valore continuo così come la scelta della velocità dell'auto.

Episodi

MDP definisce anche degli "episodi" in particolare:

Nel MDP episodico un episodio termina a determinate condizioni. Es. nel gioco degli scacchi quando la giocare da scacco matto.

Nel MDP continuo, il processo non ha fine, semplicemente continua ad esistere all'infinito in quanto non esiste uno stato fine.

Traiettoria ed episodio

La traiettoria è il movimento che l'agente compie per muoversi da uno stato all'altro. La traiettoria è definita dal simbolo greco $\tau$ "tau". Un esempio può essere:

$\tau$ = S0, A0, R1, S1,.A1, R2, S2, A2, R3, S3 che indica la partenza dallo stato zero, dove viene effettuata l'azione A0 che porta la reward R1 e il posizionamento nello stato S1, alla quale segue l'azione A1 e così via. L'ultimo stato della traiettoria sarà (nel caso specifico) S3.

L'episodio è semplicemente una traiettoria che inizia in uno stato e finisce nello stato finale oltre quale non si torna indietro. es:

$\tau$ = S0, A0, R1, S1,.A1, R2, S2, A2, R3, S3, ..... RT,ST.

di cui deriva il concetto di storia, ovvero la somatoria delle osservazioni, ricompense e azioni fino all'azione finale.

Ricompensa vs Ritorno

La ricompensa (reward) viene restituita a fronte di un'azione, quindi per risolvere un task, dobbiamo massimizzare le ricompense ottenute. La ricompensa è quindi un risultato immediato. (Rt)

Invece il ritorno è la somma di tutte le ricompense ad un determinato momento nel tempo es: G(t) = R(t+1) + R(t+2) + ... R(T) finchè il task è stato completato.

Fattore di sconto γ (gamma)

Il fattore di sconto è un incentivo per completare l'episodio nel miglior modo (più efficiente) possibile. Per ottenere questo la ricompensa dovrà essere moltiplicata per il fattore di sconto che diminuirà nel tempo all'aumentare delle azioni intraprese, rendendo le ricompense sempre più basse e quindi disincentivando le traiettorie lunghe.

Il fattore è un valore compreso tra zero e uno e viene elevato ad un esponente corrispondente dall'iesima azione fino alla fine dell'episodio.

Se γ (gamma) vale zero l'agente cercherà di prendere una ricompensa immediata, il che denota una strategia miope che non ottimizza l'apprendimento. Al contrario invece, un fattore γ gamma pari a uno, rende l'agente più "paziente" e quindi non prono ad ottimizzare gli step dell'episodio. In genere il fattore gamma viene settato a 0,99 che forza l'agente ad avere una ricompensa immediata ma allo stesso tempo lo forza ad avere una visione "a lungo termine".

In conclusione il fattore gamma indica all'agente quanto può valutare in maniera ottimali le azioni future.

Policy

La policy dell'agente è una funzione che prende in input uno stato e ritorna l'azione che va presa in quello stato. E' rappresenta dalla lettere greca pigreco .

La probabilità di eseguire un'azione (a) nello stato (s) si può rappresentare come: (a|s)

L'azione che la policy sceglie nello stato (s) viene descritta dalla formula: (s)

Dipende quindi dal contesto, in alcuni casi si uitilzza il primo (a|S) in altri il secondo (s).

La policy può essere di due tipi: stocastica o deterministica.

Si dice che la policy è deterministica quando viene scelta sempre la stessa azione in un determinato stato quindi stiamo parlando del caso (S).

Si dice invece stocastica quando l'azione viene scelta sulla base delle probabilità es. : (S) = [0.3, 0.2, 0.5] ovvero la probabilità di effettuare una azione nello stato S, è del 30% nel primo caso, 20% nel secondo e 50% nel terzo. Quindi siamo in presenza del caso (a|S)

Quindi bisogna trovare la policy ottimale rappresentata come * (pigreco - asterisco) che sceglie le azioni che massimizzano la somma dei fattori di sconto per le ricompense alla lunga.

Controllo Ottimale

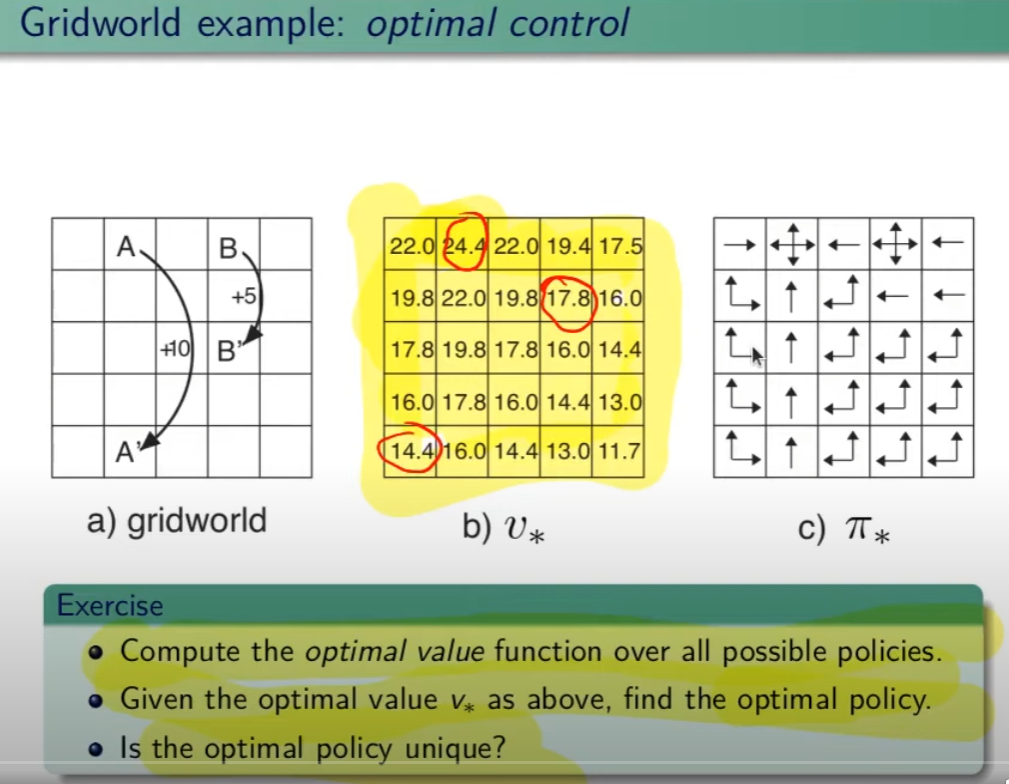
Nel RL è fondamentale determinare la Policy Ottimale indispensabile per la gestione dell'ambiente. La griglia di centro (visibile in figura) è la rappresentazione del valore di ciascuno stato. (dove per stato si intende ogni casella della griglia) Per valore ottimale V* si intende il valore della policy ottimale, ovvero quello che si può ottenere facendo le azioni migliori possibili. Per migliore azione si intende determinare lo scopo, ovvero massimizzare le somma delle ricompense (dette ritorno) ottenibili con le azioni future.

La policy ottimale quindi, si ottiene valutando di volta in volta il valore ottimale. Le policy ottimali sono tante, anche su un unico stato, vedi per es. che nella casella in fondo a sx il cui valore è 14,4 ha due policy ottimali in quanto i valori ottimali in questo specifico caso sono due.

Pianificazione e Apprendimento

L'apprendimento nel RL si basa sulla pianificazione.

La pianficazione implica la conoscenza del modello associato all'ambiente, es. il lancio di un dado che implica che il valore medio detto anche ritorno medio dell'azione è 3,5 ovvero 1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6.

NB: il modello è l'ambiente e normalmente NON lo conosciamo.

L'apprendimento, è la fase successiva alla pianificazione e implica l'iterazione con l'ambiente e prevede il calcolo della media empirica ovvero la media dei valori ottenuti dall'iterazione con l'ambiente.

Quindi con la pianficazione e l'apprendimento, l'agente migliora la policy.

Entrambi guardano avanti nel futuro calcolando i valori cercando il miglioramento della policy.

Tipologie di algoritmi applicabili al RL

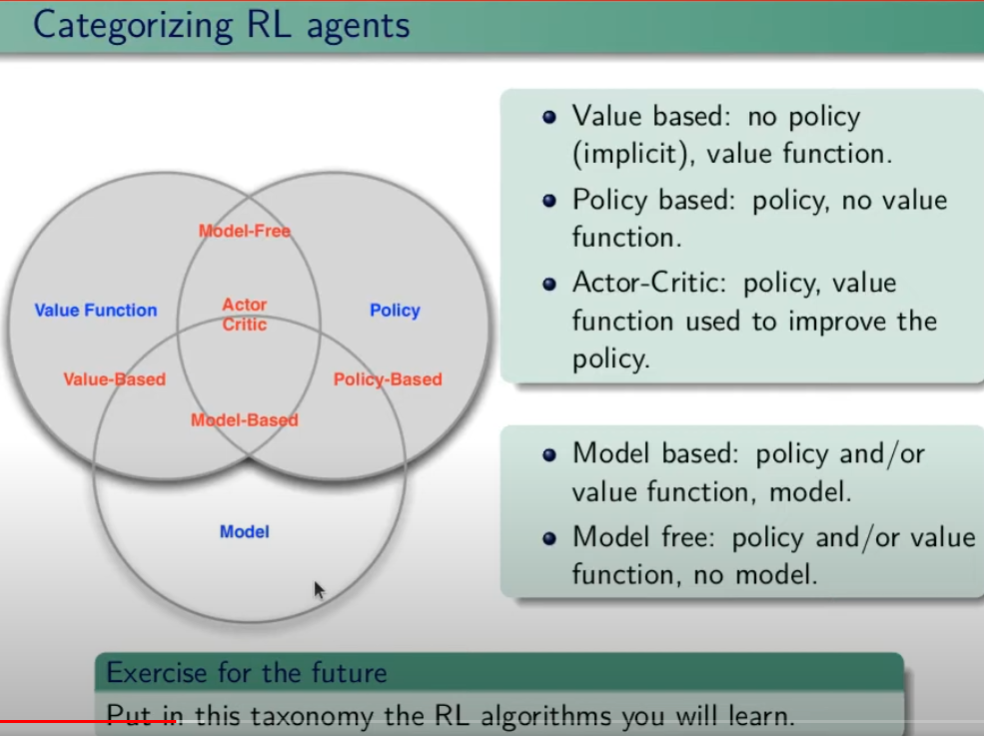
Di seguito viene rappresentata la tassonomia (categorizzazione) delle varie tipologie di algoritmi applicabili nell'ambito del RL.

Esplorazione vs Sfruttamento

E' l'eterno dilemma, ovvero provo sempre nuove soluzioni o sfrutto sempre quelle che già conosco. Entrambi vanni utilizzati per "allenare" la rete rete neurale. (vedremo più avanti)

Processi decisionali di Markov (MDP)

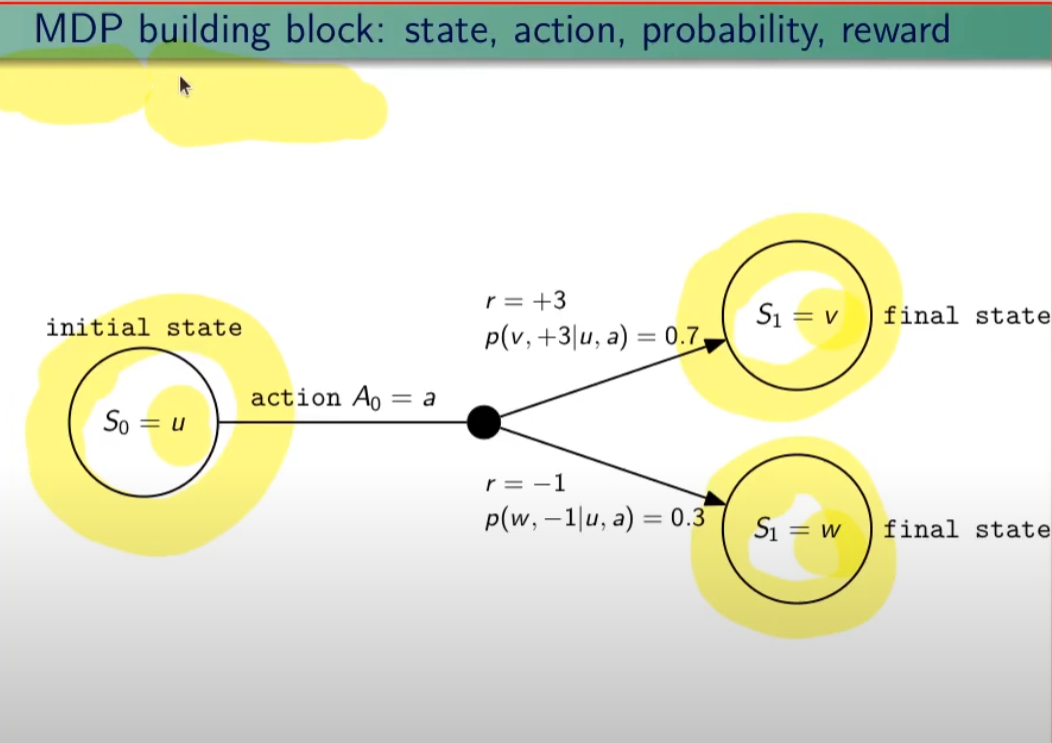
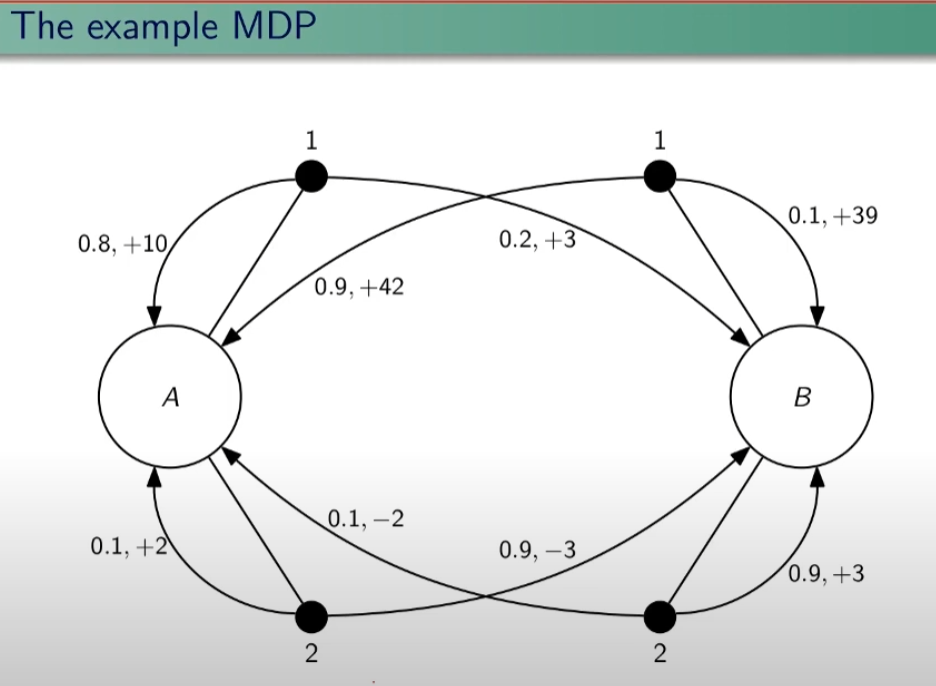
I processi decisionali di Markov si basano sulla gestione degli stati. Gli stati vengono rappresentati come dei cerchi dove all'interno è presente una lettera che lo rappresenta. Il pallino nero invece è l'azione.

Nello schema sotto rappresentato vediamo che, partendo dallo stato "u", la risposta dell'ambiente a fronte dell'azione "a" di tipo probabilistico (aleatoria) e quindi non deterministico, è di 0,7 con un reward di +3 che ci porta di v, oppure 0,3 con reward -1 che ci porta in "w". Se invece a fronte di una azione (pallino) ci fosse stato una unica determinazone della riposta dello stato T+1 anzichè due o piu, allora la risposta sarebbe stata derministica.

Es. leggendo la risposta dell'ambiente a fronte dell'azione a (nel caso dello 0,7 - 70%) è: la probabilità di arrivare in "v" con una ricompensa di +3, dato che sono partito dallo stato iniziale "u" e ho fatto l'azione "a".

Sempre rimandendo nel diagramma sopra riportato, qual'è la probabilità di andare in "w" con una reward di 42? (vedi figura sotto)

La risposta è zero in quando deve verificarsi la combinazione stato + reward che in questo caso non esistendo è quindi pari zero.

NOTA: lo stato terminale si indica con un quadrato.

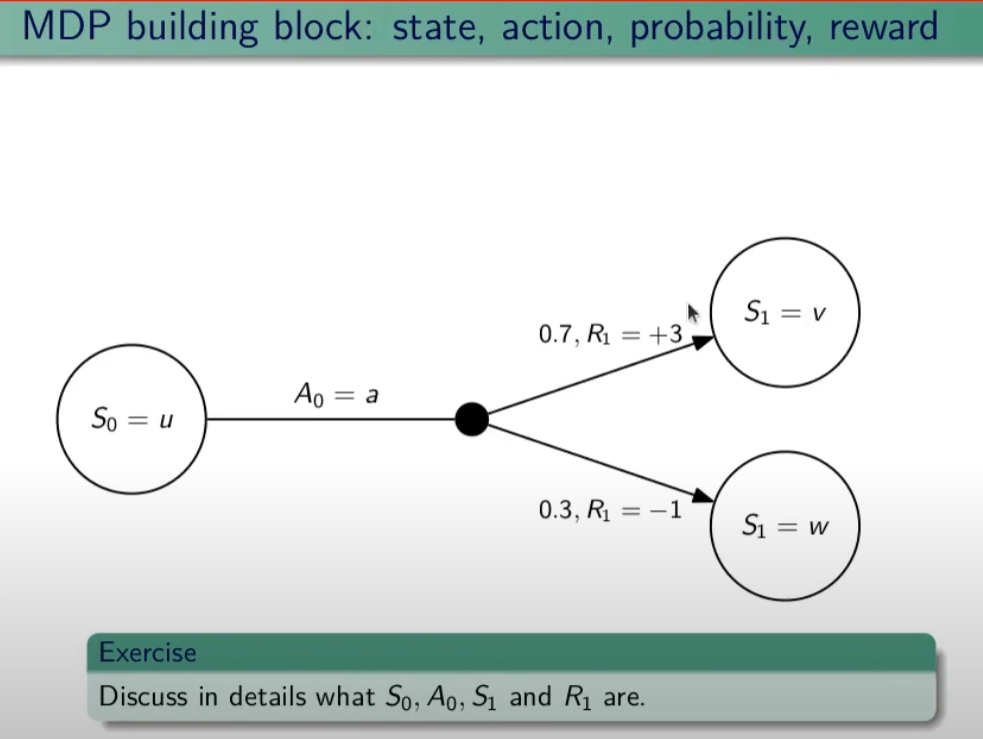
Ora semplifichiamo un attimo lo schema per renderlo più leggibile come sotto riportato:

Nello specifico la differenza tra S0 e S1 indica la situazione dello stato "S" al tempo T. Ovvero S0 è lo stato iniziale, mentre S1 è sempre lo stato S ma al tempo T+1 e può valere "w" o "v" a seconda della probabilità. Se ci fosse uno stato successivo S2 dovremmo considerare le probabilità di transizione da S0 a S1 e da S1 a S2.

La rappresentazione è quindi un grafo orientato in quanto unidirezionale. i tondi sono le azioni e gli archi i risultati probabilistici delle azioni.

Ho quindi un insieme di stati S e di azioni A e di rewards R. Dopo ogni azione ho quindi una distribuzione di probabilità su SxR. Per ogni coppia di stato azione ho una distribuzione di probabilità. Conoscere il modello significa quindi conoscere la distribuzione di probabilità. Introduciamo anche il fattore di sconto gamma che vale sempre di meno all'allungarsi della distanza di tempo in modo che l'agente sia incentivato a trovare la soluzione migliore più velocemente.

La funzione p rappresenta quindi il modello, è quindi la probabilità di transizione dallo stato al tempo T-1 allo stato al tempo T. (a fronte di una certa azioen e relativa ricompensa)

Generalizzando quanto sinora detto:

dove il simbolo (pipe) indica che un elmento "a" è condizionato a "b", es. "a" | "b".

Esercizio:

nota: ricordare che il simbolo rappresenta il ritorno atteso ovvero il valor medio dei ritorni.

La prima riga si legge così: la probabilità che un stato S al tempo T sia s' condizionato al fatto che lo stato precedente fosse s e che io abbia fatto precendetemente una derminazione azione a. Quindi si vuole sapere la probabilità di essere nello stato s' nel caso in cui nello stato precedente s sia stata eseguita l'azione a.

Per ricavare questa probabilità bisogna partire la formula generica MDP che tiene conto delle rewards, ovvero:

quindi per rispondere al prima quesito dobbiamo sommare tutte le rewards in modo che rimanga la sola probabilità che ci porta allo stato s', in quanto non vogliamo la probabilità che esca s' e r, ma vogliamo solo la probabilità che esca s', oovero:

perchè sommando tutte le rewards ho la certezza di finire nello stato s'. Sommare tutti gli "r" si dice anche saturare tutti gli indici r.

In questo caso invece si desiderata la ricompensa media (variabile aletoria) al tempo "t" condizionata dal fatto che al tempo t-1 partissi dallo stato "s" e facessi l'azione "a".

Quindi il valore medio della ricompensa sarà la sommatoria di tutte le ricompense ciascuna di esse moltiplicate per la propria probabilità di uscita, ovvero:

dato che in questo caso vogliamo la reward media al tempo t, come nel caso 1) dobbiamo "saturare" un fattore, in questo caso sono gli stati. Quindi per tutti gli stati s' moltiplichiamo la probabilità ritornata dall'azione a nello stato "s" a t-1 per tutte le reward. La prima sommatoria estrare tutte le reward che vanno a moltiplicare le corrispittive probabilità. Moltiplicando reward per la probabilità si ottinene la reward media. (vedi esempio del valotre medio del lancio del dado, dato dalla sommatoria del valore di ciacuna faccia del dado per 1/6 per un totale di 3,5)

3) per ora non viene spiegato.

Dinamica del MDP: rappresentazione tabbellare

Una delle tecniche più basiche di rappresentazione delle transizioni da uno stato all'altro fa uso di matrici di valori che indicano la probabilità di transizione da uno stato all'altro. Se per esempio un sistema ha 4 stati, la tabella sarò composta da una mtrice di 4x4. Ovviamente questo metodo funziona con sistemi i cui stati sono molto limitati, non per funziona con sistemi complessi come per es. gli scacchi o la dama.

Facciamo un esempio, calcoliamo su questo MDP delle quantità:

Iniziamo con il calcolo di una matrice di transizione detta matrice stocastica, in queso caso avendo due stati la matrice è 2x2, nelle celle della matrice andremo ad inserire le probabilità di transizione da uno stato all'altro. Nell'esempio sotto riportato andremo a calcolare la matrice associata all'azione 1. La peculiarità di questa matrice è che la somma di ciascuna riga da sempre 1 - 100%.

P = 1 (azione 1)	A	B
A	0,8	0,2
B	0,9	0,1

Calcoliamo ora il vattore ricompensa associata all'azione 1.

R = 1 (azione 1)

10*0,8 + 3*0,2 = 8,6

0,9*42+0,1*39 = 41,7

ora creiamo che tabella che rappresenta l'intero modello:

s (stato partenza)	a (azione)	s' (stato di arrivo)	r (ricompensa)	p(s',r \| s,a) probabilità
A	1	B	3	0,2
...

La tabella conterrà un totale di righe dato dalle azioni x numero di probabilità di accedere allo stato, questo caso 8.

La proprietà di "Markovianità"

La proprità di markov indica che il valore dello stato St dipende esclusivamente dallo St-1 ma non dipende dagli stati precedenti a St-1. (es. St-2, St-3 etc etc)

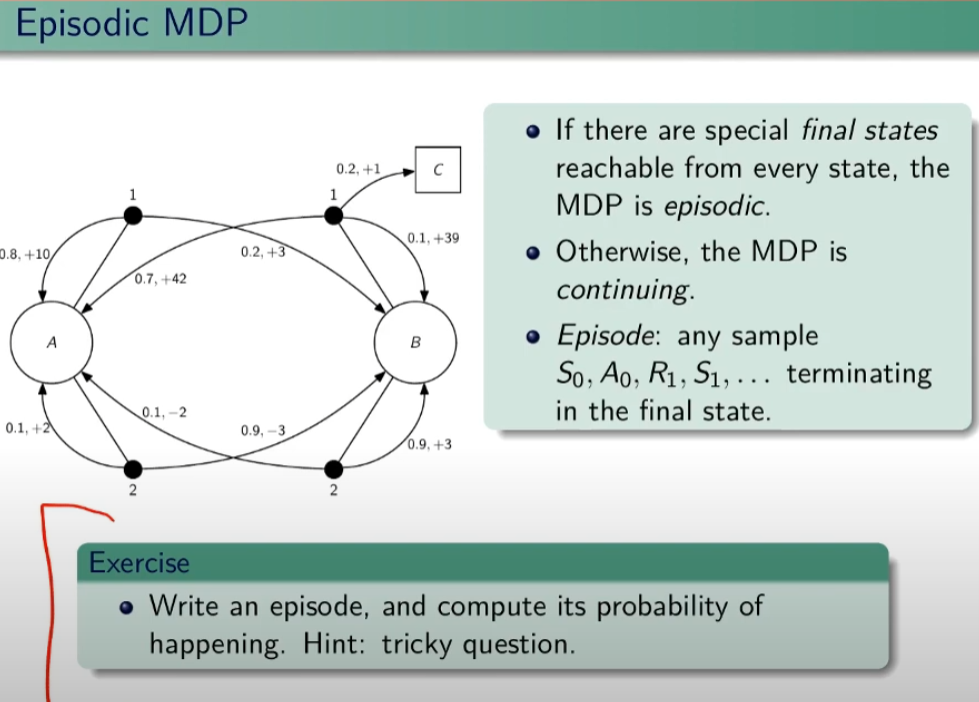
Episodi MDP

Se ho uno stato terminale tra gli stati possibili allora il mio task si chiama episodico. Attenzione che però dipende dalla policy, ovvero se ho delle azioni che mi consentono di evitare lo stato terminali posso entrare in loop. E' compito dell'algoritmo evitare questi loop. Nel caso in cui non esista lo stato terminale si tratta di un MDP continuing.

Esiston anche task a orizzonte temporale definito se esistono dei limiti temporali.

Un episodio quindi è una sequenza di stati, azioni, rewards che terminano con lo stato terminale.

Simuliamo un episodio:

EPISODIO: A, 1,10, A, 2, -3, B, 2, 0,9, B , 1, 1, C

PROBABILITA': dipende da:

probabilità di scegliere (1|A)
probabilità di scegliere (2|A)
probabilità di scegliere (1|B)
probabilità di scegliere (2|B)

Per calcolare un episodio bisogna capire quindi come viene definita la policy.

Un esempio di policy che per esempio può essere scegliere sempre l'azione 1. Quindi la policy "pi" è fondamentalmente una strategia che può (e spesso deve) variare per massimizzare il ritorno.

Ritorno

Il ritorno (G = gain) è la somma delle ricompense di un episodio ed è una variabile aleatoria.

NB: L'ipotesi è che i ritorni R abbiamo un limite superiore finito che consente al fattore di sconto far convergere il ritorno totale.

2019 10 28

Ricordo la notazione che si ripeterà spesso nel corso, 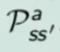ovvero la probabilità che facendo un'azione "a" nello stato "s" l'ambiente mi porti nello stato s'. Il mio comportamento è rappresentato da una distribuzione di probabilità negli stati S. La strategia di scelta delle azioni - che sia chiama polocy - è una distribuzione di probabilità neglis stati.

Le policy ottimali possono essere deterministiche o non deterministiche. Un esempio di policy determinisca è il lancio de dado in quanto ho una sola possibile azione, appunto il lancio del dato, invece un esempio di non deterministica è per es. sasso-carta-forbice.

Funzione stato-valore

La funzione stato valore per un MDP è il numero che ci indica quale azione intraprendere. Si rappresenta come:

dove V è il valore indicizzato dalla lettera pi (policy) indicizzato dallo stato S.

Mentre "E" è il valore atteso, è il valore dello stato, è il numero teorico che se lo conoscessimo aprioristicamente ci "renderebbe la vita più semplice" in quanto significherebbe che conosceremmo l'ambiente, cosa ovviamente non possibile.

"E" il è il valore che voglio massimizzare, viene quindi indicato con la lettera "V" che sta per valore indicizzato a pi-greco ovvero la "policy" cioè quello che facciamo noi espresso in probabilità di effettuare un'azione, dello stato "S" (notazione funzionale) uguale al valore medio atteso di Gt -> ritorno al tempo "t" condizionato al stato "s" che è l'argomento della funzione V( s)

Q-learning

E ora veniamo ad un concetto molto importante, il concetto del Q-learning, ovvero action value function che sta per qualità dell'azione.

Una piccola premessa, V( s) è il valore atteso applicando la policy pi (pigreco) nello stato "s", mentre invece l'azione valore Q( s,a) è il valore atteso partendo dallo stato "s" e scegliendo l'azione "a" applicando la policy "pi". (vedi immagine sotto riportata) Nel caso di Vpi(s) abbiamo il valore atteso nello stato "s" (nb: specifico stato "s", non altri) applicando un'azione casuale, nentre con Qpi(s,a) abbiamo si il ritorno nello stato "s" ma applichiamo l'azione "a" in modo che il ritorno sia massimizzato, quindi la differenza rispetto a Vpi(s) è che nel primo caso l'azione è casuale (e per questo non compare nella formula) mentre nel Qpi(s,a) l'azione scelta è quella con maggior probabilità ci restituire un ritorno massimizzato. Quindi viene valutata la "qualità" dell'azione "a".

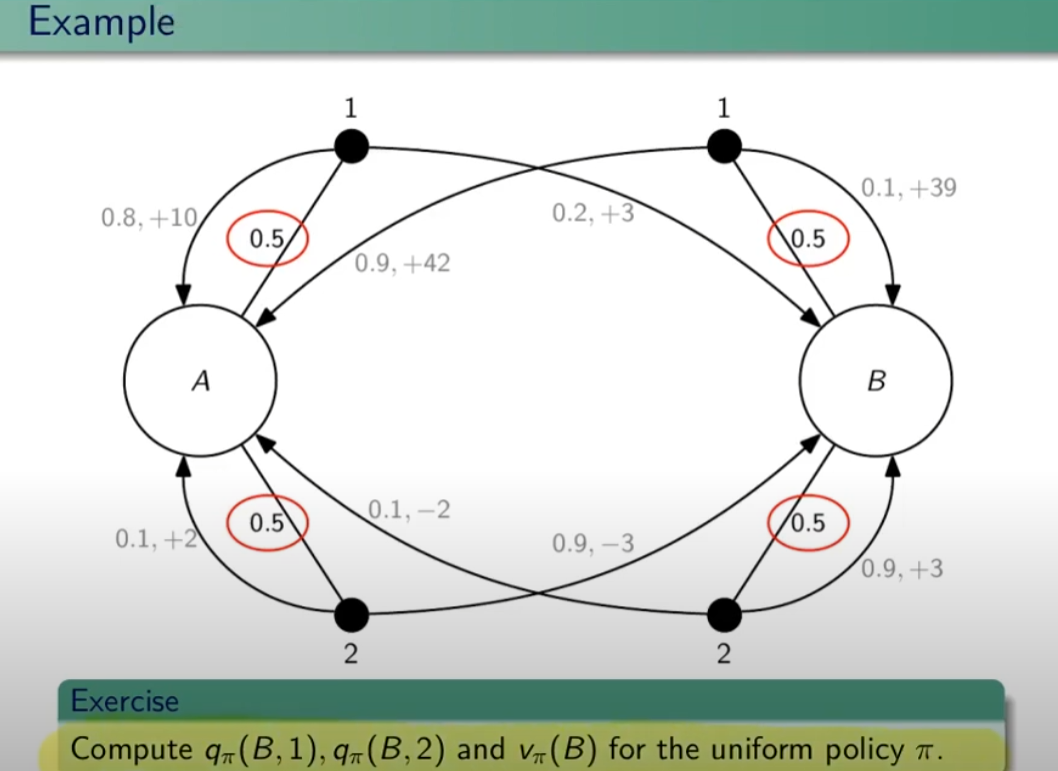
Ora facciamo un esempio:

Esercizio: calcolare il q-values applicando la policy pi nello stato B e compiendo l'azione 1 in un caso e l'azione 2 nell'altro; e calcolare il valore atteso nello stato B applicando la policy uniforme pi.

Soluzione q_pi(B,1)

q_pi(B,1) = 0,1*(gamma*39+ gamma*V_pi(B)) + 0,9*(gamma*42+gamma*V_pi(A))

dove:

V_pi(B) = 0,5*q_pi(B,1)+0,5*q_pi(B,2)

V_pi(A) = 0,5*q_pi(A,1)+0,5*q_pi(A,2)

spiegone:

Per determinare la funzione q (valore azione) relativa alla policy pi che nel caso di partenza da B, è necessario applicare la "policy di partenza" ovvero al 50% di probabilità di scegliere un'azione. Quindi la q_pi(B,1) è calcolata come la probabilità di scegliere l'azione 1 (che in questo caso è del 100% in quanto viene impostato come richiesta iniziale) che moltiplica la probabilità del 10% di ottenere 39 sommato al valoree-pi dello stato di arrivo ovvero "B", più la probabilità del 90% di andare nello stato A ottenedo 42 sommato al valore-pi di A.

Il valore-pi di A è a sua volta la probabilità di scegliere l'azione 1 sommata alla probabilità di scegliere l'azione 2 ovvero: V_pi(A) = 0,5*q_pi(A,1)+0,5*q_pi(A,2). (dove la provabilità per questa policy di scegliere l'azione è del 50%)

Analogamente il valore-pi di B è probabilità di scegliere l'azione 1 sommata alla probabilità di scegliere l'azione 2 ovvero: V_pi(B) = 0,5*q_pi(B,1)+0,5*q_pi(B,2). (dove la provabilità per questa policy di scegliere l'azione è del 50%)

Da notare che questa non è la policy ottimale in quanto è la policy di partenza che ci da il 50%, l'apprendimento sta nell'iterare il processo a fine di variare la % della policy per farla convergere a quella ottimale.

Bisogna quindi calcolare di 4 equazione a 4 incognite che sono: q-pi(A,1) q-pi(A,2) q-pi(B,1) e q-pi(B,2)

Per farla convergere però, bisogna utilizzare un fattore di sconto gamma, altrimenti tende a infinito... (di qui l'introduzione di gamma)

Questo ciclo (iterazione) viene anche detto controllo.

In conclusione questo sistema è una versione dell'equazione di Bellman.

Equazione di Bellman

Il ritorno Gt può essere formulato (descritto) in maniera ricorsiva in quanto è la somma delle ricompense. Ovvero il ritorno al tempo t è la somma della ricompensa al tempo t+1 sommato al ritorno del tempo t+1, dove il ritorno al tempo t+1 rispetto a t+1 (scontato di gamma ovviamente)

Ovvero:

da qui l'equazione di Bellman:

innanzitutto bisogna osservare che è un'equazione ricorsiva, in quanto all'interno della funzione è riproposta la funzione stessa.

Dimostriamola:

partiamo dall'assunto:

che ci dice che il valore-pi allo stato S è pari al valore atteso dato dal ritorno al tempo t subordinato allo stato "s".

V_pi(S) =

2019 10 29

-------------------

Valutazione degli stati e delle azioni di un task

Per valutare il ritorno totale di un'azione nello stato:

Q(s,a) = E[Gt|St=s, At = a]

ovvero: Il valore Q di un'azione rappresenta il ritorno che ci aspettiamo se iniziano dallo stato s eseguendo l'azione a e interagiamo con l'ambiente (E) seguendo la policy fino alla fine dell'episodio.

L'equazione di Bellman per v(s)

Dalla prima equazione sotto riportata si evince che il ritorno atteso utilizzando la policy ottimale è dato dal ritorno dello stato T. Espandando la definzione, come si evince dalla seconda equazione, viene rappresentato il ritorno ottimale partendo dallo stato successivo fino a quello finale scontato del fattore gamma.

Veniamo quindi all'equazione generica (la quarta) che indica la probabilità di eseguire ciascuna azione sulla base della policy moltiplicata dal ritorno atesso dal eseguire l'azione.

Con le nozioni di Equazione di Bellman e di Markov Decision Process possiamo finalmente sviscerare il concetto di Q-Learning.

Fin’ora abbiamo cercato di calcolare V(s), con il quale derivare la migliore azione da compiere in funzione dello stato corrente.

Ora invece di considerare il valore di ogni stato V(s), prendiamo il valore della coppia stato-azione che indichiamo con Q(s,a).

Intuitivamente, possiamo pensare al Q-value come la “qualità”dell’azione.

La nostra equazione diventa quindi:

Compiendo un’azione, il nostro agente riceve inizialmente una ricompensa R(s,a) .

Ora poiché il nuovo stato può esse uno tra molti, aggiungiamo il calcolo del valore atteso nello stato successivo.

Per cui il valore dello stato V(s) assume il massimo valore tra tutti i possibili Q-values.

Con una semplice modifica, otteniamo dunque la formula ricorsiva per il calcolo del Q-Value.

Sappi che, sebbene l’esempio sia caratterizzato da uno spazio azioni e stati discreto, lo stesso ragionamento può essere applicato a uno spazio azioni e stati continuo, generalmente dividendo il continuo in intervalli discreti.

∑ TBD

Riassumendo

Il Reinforcement Learning è un processo caratterizzato a livello macro da due entità:

Un ambiente (environment) che semplifica una certa realtà;
Un agente (agent), tecnicamente un modello di AI (e.g. rete neurale) che interagisce con l’ambiente.

Ci sono altri tre termini chiave nel vocabolario del Reinforcement Learning che bisogna necessariamente conoscere.

L’agente interagisce con l’ambiente, per realizzare ciò, compie azioni (actions) che alterano l’ambiente (anche se non è sempre così) generando un nuovo stato (state), ottenendo una ricompensa (reward) che può essere negativa o positiva in base all’effetto dell’azione, e in funzione del risultato desiderato.

Compiendo azioni e ottenendo ricompense, l’agente elabora una strategia ottimale per massimizzare la ricompensa nel tempo. Questa strategia è definita policy, ed è una funziona matematica a parametri ottimizzati.

Bellman Equation per Q-Learning

L’Equazione di Bellman è un concetto fondamentale nel Renforcement Learning,

Fu introdotta nel 1954 dal Richard Bellman, conosciuto come il padre del Dynamic Programming, in una pubblicazione intitolata The Theory of Dynamic Porgramming.

Partiamo da un Toy Problem, un problema piccolo e utile solo a capire i concetti di fondo.

Consideriamo un piccolo robot che debba raggiungere la posizione finale di un percorso evitando gli ostacoli:

Potremmo quindi configurare un sistema a ricompense specifico per l’ambiente tale per cui:

-1 per ogni step (Per incoraggiare l’agente a raggiungere l’obiettivo percorrendo la tratta più breve)
-100 per ogni mina
+1 per ogni fulmine
+100 per il raggiungimento della fine.

Per risolvere questo problema, dobbiamo introdurre il concetto di Q-Table.

Q-Table

Una Q-Table è una lookup table che calcola il valore atteso delle ricompense future per ogni azione in ogni possibile stato. Questo permette all’agente di scegliere la migliore azione in ogni stato.

Il nostro ambiente ha 4 possibili azioni (sopra, sotto, destra, e sinistra) e 5 possibili stati (inizio, vuoto, fulmine, mina, fine).

La domanda è dunque: come calcoliamo la massima ricompensa possibile per ogni stato, ovvero i valori della Q-Table?

Abbiamo bisogno di un processo iterativo che faccia uso del Q-Learning algorithm, il quale a sua volta si appoggia all’equazione di Bellman.

E il cerchio si chiude.

L’Equazione di Bellman per sistemi deterministici è la seguente:

In cui abbiamo:

s – State
α – Action
R – Reward
γ – Discount factor

Il fattore di sconto è necessario per tarare la variazione della ricompensa nel tempo, comunicando all’agente quanto sia rilevante la ricompensa presente rispetto a quella futura.

C’è però una questione limitante nell’applicare l’equazione a qualsivoglia ambiente.

La formula funziona solamente quando è noto lo stato successivo, informazione spesso sconosciuta e anzi dipendente dall’azione compiuta.

Abbiamo quindi bisogno di un sistema per modellare ambienti in qualche modo legati a un fattore casuale, non prevedibile.

Ora che abbiamo un’infarinatura sul concetto di Q-Table, passiamo quindi al prossimo: i Markov Decision Processes

Markov Decision Processes (MDPs) in Q-Learning

Dobbiamo distinguere due tipologie di ambiente:

Ambiente Deterministico, per ogni azione compiuta dall’agente la probabilità che questa avvenga correttamente è massima (100%)
Ambiente non deterministico, per ogni azione compiuta dall’agente la probabilità che questa avvenga è influenzata da un fattore casuale, ed è quindi incerta.

Ora possiamo allora introdurre il concetto di processo di Markov e processo decisionale di Markov.

Il Markov Decision Process (MDP) o processo decisionale di Markov è un modello di gestione dello stato di transizione di un agente in un ambiente dinamico e casuale, dunque non deterministico.

Fornisce un modello matematico per modellare un processo decisionale in quelle situazioni in cui il risultato è parzialmente casuale (random), e in parte sotto controllo di un decisore (decision maker).

Una definizione molto comoda per compiacere il nostro interlocutore, ma poco utile per comprendere a fondo il significato di questo concetto.

Scopriamo insieme in cosa consiste il Markov Decision Process, e sopratutto perché sia importante.

Markov Decision Process

Per capire a fondo cosa sia un processo decisionale di markov dobbiamo fare chiarezza su almeno due conceti:

La catena di Markov, o Markov chain
La proprietà di Markov o Markov property

Iniziamo dal primo.

Markov Chain

Nei primi anni del secolo scorso, il matematico russo Andrej Markov studiò i processi stocastici, che involvono un elemento di casualità, senza memoria, chiamati catene di Markov o Markov Chains.

Un tale processo ha un numero fisso di stati, ed evolve in modo casuale da uno stato all’altro, a ogni step.

La probabilità che l’evoluzione avvenga dallo stato s a quello s’ è fissa e dipende unicamente dalla coppia (s, s’) e non dagli stati passati, ergo per cui definiamo il sistema come privo di memoria.

Privo di memoria?

No, non ha bevuto la sera prima e dimenticato la festa in spiaggia tornando a casa con un male alla testa da Guiness World Record.

Possiamo però fare chiarezza sull’argomento.

Markov Property

Tecnicamente, l’indipendenza dagli stati passati in un processo stocastico è definita in Teoria della Probabilità come Markov property, trovi un approfondimento qui.

La Markov Property è il discriminante per distinguere i Markov Process.

Diciamo infatti che un processo stocastico si definisce Markov Process se e solo se risulti caratterizzato dalla Markov Property, e quindi se la distribuzione di probabilità condizionata dei futuri stati del processo (condizionata su entrambi gli insiemi di stati futuri e passati) dipende unicamente dallo stato presente e non dalla sequenza di eventi precedenti.

Devi sapere anche un’altra cosa fondamentale.

Da un punto di vista matematico, un processo stocastico altro non è che una famiglia di variabili casuali (i.e. Il cui valore dipende da un fenomeno aleatorio, cioè casuale) indicizzate da un parametro temporale.

Distinguiamo allora un processo stocastico tempo-discreto (o tempo-continuo) a seconda che lo spazio della variabile tempo sia discreto (o continuo).

Ora hai tutti gli strumenti per capire cosa sia davvero una Markov chain: un processo stocastico tempo-discreto (i.e. Discreto nel tempo) che soddisfa la Markov property.

Le Markov chains sono utilizzate in molte aree, tra cui termodinamica, chimica, statistica e altre.

Vediamo ora cosa sia un Markov decision process.

Markov Decision Processes

Fu Richard Bellman a descrivere per la prima volta i Markov Decision Processes in una celebre pubblicazione degli anni ’50.

I Markov Decision Processes sono allora un’estensione delle Markov Chains, con due aggiunte:

Azioni, actions (i.e. Permettono una scelta)
Ricompense, rewards (i.e. Motivano l’agente)

Quando esiste una sola azione per ogni step, e tutte le ricompense sono uguali, il processo decisionale di Markov (Markov decision process) si riduce a una catena di Markov (Markov chain).

Osserviamo allora un esempio di Markov decision process.

Il MDP in figura ha 3 stati e al massimo 3 azioni per ogni step.

Iniziando allo stato s₀ l’agente può scegliere una delle 3 azioni a₀,a₁,a₂.

Se scegliesse l’azione a₁ rimarrebbe nello stato s₀ con certezza (probabilità 1.0) senza ottenere alcuna ricompensa.

Se scegliesse l’azione a₀, avrebbe il 70% di probabilità di guadagnare una ricompensa di 10 punti e rimanere nello stato s₀. In questo caso l’agente potrebbe optare per la medesima scelta ottenendo quante più ricompense possibili, benché a un certo punto raggiungerà lo stato s₁.

Nello stato s₁ le azioni sono 2: a₀ e a₂.

L’agente può ora scegliere di stare ripetutamente nello stato optando per l’azione a₀. L’azione a₂ permetterebbe invece all’agente di raggiungere lo stato s₂ seppur con una ricompensa negativa di 50 punti.

Dallo stato s₂ la sola azione concessa è l’a₀ che riporterebbe l’agente allo stato iniziale con una ricompensa di 40 punti.

Bellman individuò un modo per stimare un parametro, l’optimal state value di qualunque stato s, espresso come V*(s) inteso come somma di tutte le future ricompense scontate (i.e. Con applicato il discount rate, spiegato in questo post) che l’agente può potenzialmente ricevere in media dopo aver raggiunto lo stato s, assumendo che agisca in modo ottimale.

Bellman dimostrò che quando l’agente agisce in modo ottimale, la Bellman Optimality Equation può essere applicata.

Si tratta di un’equazione ricorsiva che, assumendo che l’agente agisca in modo ottimale, permette il calcolo dell’optimal state value, dello stato corrente come la somma delle ricompense che potrebbe ottenere in media optando per l’azione ottimale e la stima dell’optimal state value di tutti i possibili stati a cui l’azione designata porterebbe.

Questa equazione conduce a un algoritmo in grado di stimare precisamente l’optimal state value di ogni possibile stato: inizializzando ogni parametro a zero, e aggiornandoli iterativamente usando il Value Iteration Algorithm.

Il punto di forza di questo metodo è la garanzia che i valori stimati convergano all’optimal state values di ogni stato, costituendo dunque la policy ottimale.

Processo di Markov è tale quando presenta la proprietà di Markov, quando cioè la distribuzione di probabilità dei futuri stati del processo dipendono unicamente dallo stato presente e non dalla serie di eventi a esso preceduti.

I processi decisionali di Markov costituiscono invece un framework per modellare, sotto specifiche condizioni, un atto di Decision Making, in quelle situazioni in cui il risultato è in parte casuale e in parte sotto il controllo del decision maker.

Applicando questi concetti all’Equazione di Bellman, otteniamo una variante per ambienti non deterministici:

Q-Learning

Con le nozioni di Equazione di Bellman e di Markov Decision Process sulle spalle possiamo finalmente sviscerare il concetto di Q-Learning.